第5页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 例 3 把下列各数分别填入相应的集合:
$0$,$-3$,$-8\frac{1}{4}$,$\frac{2}{7}$,$-0.020 020 002$,$15$,$365\%$.
(1)整数集合:…$\{ $
(2)正有理数集合:…$\{ $
(3)负有理数集合:…$\{ $
$0$,$-3$,$-8\frac{1}{4}$,$\frac{2}{7}$,$-0.020 020 002$,$15$,$365\%$.
(1)整数集合:…$\{ $
$0$,$-3$,$15$
$\}$;(2)正有理数集合:…$\{ $
$\frac{2}{7}$,$15$,$365\%$
$\}$;(3)负有理数集合:…$\{ $
$-3$,$-8\frac{1}{4}$,$-0.020 020 002$
$\}$.
答案:
解析 0 是整数,$-3$是整数、负有理数,$-8\frac{1}{4}$是负有理数,$\frac{2}{7}$是正有理数,$-0.020 020 002$是负有理数,15 是整数、正有理数,$365\%$是正有理数.
答案
(1)$0$,$-3$,$15$
(2)$\frac{2}{7}$,$15$,$365\%$
(3)$-3$,$-8\frac{1}{4}$,$-0.020 020 002$
答案
(1)$0$,$-3$,$15$
(2)$\frac{2}{7}$,$15$,$365\%$
(3)$-3$,$-8\frac{1}{4}$,$-0.020 020 002$
1. 在$-2$,$3.14$,$\frac{22}{7}$,$0.101 001 000…$,$0.141 4$中,有理数的个数是(
A.5
B.4
C.3
D.2
B
)A.5
B.4
C.3
D.2
答案:
B
2. 在有理数中,不存在这样的一个数,它(
A.既是自然数,又是整数
B.既是分数,又是负数
C.既不是正数,也不是负数
D.既是正数,又是负数
D
)A.既是自然数,又是整数
B.既是分数,又是负数
C.既不是正数,也不是负数
D.既是正数,又是负数
答案:
D
3. 下列说法中:①0 是最小的整数;②有理数不是正整数就是负数;③$2.\dot{3}$是正有理数.其中正确的个数是(
A.0
B.1
C.2
D.3
B
)A.0
B.1
C.2
D.3
答案:
B
4. 根据下面的集合示意图,下列选项中的数,可填入$M$区域(两个集合的公共部分)的是(
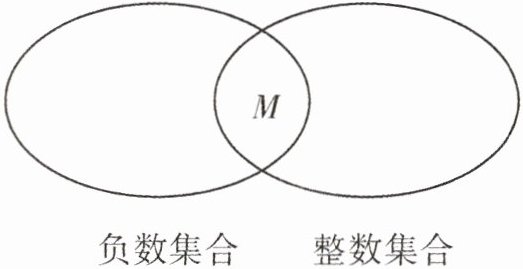
A.$-1$
B.$\frac{1}{2}$
C.$-1.5$
D.$0$
A
)
A.$-1$
B.$\frac{1}{2}$
C.$-1.5$
D.$0$
答案:
A 解析 由题意可得 M 区域(两个集合的公共部分)内的数应该是负整数,选项中只有-1 是负整数.
查看更多完整答案,请扫码查看


