第96页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
1. 甲地 6 月连续 5 日的平均气温(单位:℃)为 24,30,28,26,22,则甲地平均气温的离差平方和为
40
.
答案:
40
2. 已知一个样本数据为 2,3,4,5,6,则这组数据的方差和标准差分别是
2,$\sqrt{2}$
.
答案:
$2,\sqrt{2}$
3. 甲、乙两位同学在本学期的几次数学测试中,他们成绩的平均数相等,方差分别为 $ s_{甲}^{2}= 6.5 $, $ s_{乙}^{2}= 5.4 $,则成绩较稳定的是
乙
(填“甲”或“乙”).
答案:
乙
4. 如图,这是甲、乙两人 5 次投篮成绩统计图(每人每次投球 10 个),则对于方差的描述正确的是(
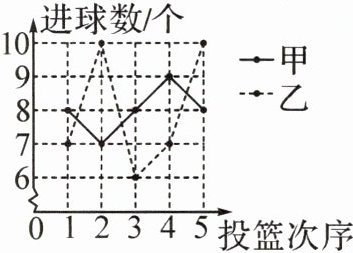
A.$ s_{甲}^{2}<s_{乙}^{2} $
B.$ s_{甲}^{2}= s_{乙}^{2} $
C.$ s_{甲}^{2}>s_{乙}^{2} $
D.无法确定
A
)
A.$ s_{甲}^{2}<s_{乙}^{2} $
B.$ s_{甲}^{2}= s_{乙}^{2} $
C.$ s_{甲}^{2}>s_{乙}^{2} $
D.无法确定
答案:
A
5. 八(1)班组织了一次食品安全知识竞赛,甲、乙两队各 5 人的成绩如下表所示(10 分制).

(1)乙队成绩的众数是
(2)分别计算甲队、乙队的方差,并判断哪队的成绩更稳定.为什么?

(1)乙队成绩的众数是
8
分.(2)分别计算甲队、乙队的方差,并判断哪队的成绩更稳定.为什么?
$\overline{x}_{甲}=\frac{1}{5}×(8+10+9+6+9)=8.4$,$s^{2}_{甲}=\frac{1}{5}×[(8-8.4)^{2}+(10-8.4)^{2}+(9-8.4)^{2}+(6-8.4)^{2}+(9-8.4)^{2}]=1.84$。$\overline{x}_{乙}=\frac{1}{5}×(10+8+9+7+8)=8.4$,$s^{2}_{乙}=\frac{1}{5}×[(10-8.4)^{2}+(8-8.4)^{2}+(9-8.4)^{2}+(7-8.4)^{2}+(8-8.4)^{2}]=1.04$。$\because s^{2}_{甲}>s^{2}_{乙}$,$\therefore$ 乙队的成绩更稳定。
答案:
(1)8 (2)$\overline{x}_{甲}=\frac{1}{5}×(8+10+9+6+9)=8.4$,$s^{2}_{甲}=\frac{1}{5}×[(8-8.4)^{2}+(10-8.4)^{2}+(9-8.4)^{2}+(6-8.4)^{2}+(9-8.4)^{2}]=1.84$。$\overline{x}_{乙}=\frac{1}{5}×(10+8+9+7+8)=8.4$,$s^{2}_{乙}=\frac{1}{5}×[(10-8.4)^{2}+(8-8.4)^{2}+(9-8.4)^{2}+(7-8.4)^{2}+(8-8.4)^{2}]=1.04$。$\because s^{2}_{甲}>s^{2}_{乙}$,$\therefore$ 乙队的成绩更稳定。
6. 某校有甲、乙两个模特队,两队人数一样,队员的平均体重都为 50 kg,离差平方和分别是 $ S_{甲}^{2} $, $ S_{乙}^{2} $,且 $ S_{甲}^{2}>S_{乙}^{2} $,则两个队的队员的体型较整齐的是(
A.甲队
B.两队一样整齐
C.乙队
D.不能确定
C
)A.甲队
B.两队一样整齐
C.乙队
D.不能确定
答案:
C
7. 某排球队 6 名场上队员的身高(单位:cm)是 180,182,184,186,190,194.现用一名身高为 188 cm 的队员换下场上身高为 194 cm 的队员,与换人前相比,场上队员的身高(
A.平均数变大,方差变大
B.平均数变大,方差变小
C.平均数变小,方差变大
D.平均数变小,方差变小
D
)A.平均数变大,方差变大
B.平均数变大,方差变小
C.平均数变小,方差变大
D.平均数变小,方差变小
答案:
D
8. 一组数据 $ x_{1} $, $ x_{2} $,…, $ x_{n} $ 的平均数为 5,方差为 16,n 是正整数,则另一组数据 $ 3x_{1}+2 $, $ 3x_{2}+2 $,…, $ 3x_{n}+2 $ 的标准差是
12
.
答案:
12
9. 某中学九年级学生共进行了五次体育模拟测试.已知甲、乙两位同学五次模拟测试成绩的总分相同,小明根据甲同学的五次测试成绩绘制了尚不完整的统计表,并给出了乙同学五次测试成绩的方差的计算过程.
甲同学五次体育模拟测试成绩统计表

小明将乙同学五次模拟测试成绩直接代入方差公式,计算过程如下: $ s_{乙}^{2}= \frac{1}{5}[(36 - 38)^{2}+(38 - 38)^{2}+(37 - 38)^{2}+(39 - 38)^{2}+(40 - 38)^{2}]= 2 $.
根据上述信息,解答下列问题:
(1)a 的值是______
(2)根据甲、乙两位同学这五次模拟测试成绩,你认为谁的体育成绩更稳定?并说明理由.
(3)如果甲再测试 1 次,第六次模拟测试成绩为 38 分,与前 5 次相比,甲 6 次模拟测试成绩的标准差______
甲同学五次体育模拟测试成绩统计表

小明将乙同学五次模拟测试成绩直接代入方差公式,计算过程如下: $ s_{乙}^{2}= \frac{1}{5}[(36 - 38)^{2}+(38 - 38)^{2}+(37 - 38)^{2}+(39 - 38)^{2}+(40 - 38)^{2}]= 2 $.
根据上述信息,解答下列问题:
(1)a 的值是______
39
.(2)根据甲、乙两位同学这五次模拟测试成绩,你认为谁的体育成绩更稳定?并说明理由.
乙的体育成绩更好。理由:$\because \overline{x}_{甲}=\frac{1}{5}(35+39+37+39+40)=38$(分),$s^{2}_{甲}=\frac{1}{5}[(35-38)^{2}+(39-38)^{2}+(37-38)^{2}+(39-38)^{2}+(40-38)^{2}]=3.2$,$\therefore s^{2}_{乙}<s^{2}_{甲}$。乙的成绩更稳定。
(3)如果甲再测试 1 次,第六次模拟测试成绩为 38 分,与前 5 次相比,甲 6 次模拟测试成绩的标准差______
变小
.(填“变大”“变小”或“不变”)
答案:
(1)39 (2)乙的体育成绩更好。理由:$\because \overline{x}_{甲}=\frac{1}{5}(35+39+37+39+40)=38$(分),$s^{2}_{甲}=\frac{1}{5}[(35-38)^{2}+(39-38)^{2}+(37-38)^{2}+(39-38)^{2}+(40-38)^{2}]=3.2$,$\therefore s^{2}_{乙}<s^{2}_{甲}$。乙的成绩更稳定。 (3)变小
查看更多完整答案,请扫码查看


