《2025年同步精练广东八年级数学上册北师大版》

1. 某水果店推出的一款水果拼盘套餐受到了广大消费者的喜爱,每天的销售量 $ y $(盒)与销售单价 $ x $(元)之间存在一次函数关系(如下表所示)。已知该水果拼盘套餐的成本为 30 元/盒。

(1) 求出 $ y $ 与 $ x $ 之间的关系式。
(2) 当销售单价为 65 元时,求当天的销售利润。(销售利润 $ =$ 销售额 $ -$ 成本)

答案： 1.解:
(1)设y与x之间的关系式为y=kx+b.由题意,得{40k+b=220,50k+b=200,解得{k=-2,b=300,
∴y与x之间的关系式为y=-2x+300.
(2)由
(1)可知,当x=65时,y=-2×65+300=170,
∴65×170-30×170=5950(元).答:当销售单价为65元时,当天的销售利润为5950元.

2. 某公司开发出一款新的节能产品,该产品的成本价为 6 元/件。该产品在正式投放市场前通过代销点进行了为期一个月(30 天)的试销售,售价为 8 元/件。工作人员对销售情况进行了跟踪记录,并将记录情况绘成图象(如图所示),图中的折线 $ ODE $ 表示日销售量 $ y $(件)与销售时间 $ x $(天)之间的函数关系。已知线段 $ DE $ 表示的函数关系中时间每增加 1 天,日销售量减少 5 件。
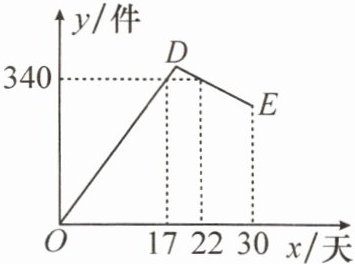
(1) 第 17 天的日销售量是340件,日销售利润是______680元。
(2) 求试销售期间日销售利润的最大值。

答案： 2.解:
(1)340 680
(2)根据图象易得,直线OD的表达式为y=20x,直线DE的表达式为y=-5x+450.联立{y=20x,y=-5x+450,解得{x=18,y=360,
∴折线ODE的最高点D的坐标为(18,360).360×(8-6)=720(元),
∴当x=18时,日销售利润最大,最大利润为720元.

3. 甲、乙两个工程组同时挖掘沈白高铁某段隧道,两组每天挖掘长度均保持不变。合作一段时间后,乙组因维修设备而停工,甲组单独完成了剩下的任务。甲、乙两组挖掘的长度之和 $ y $(m)与甲组挖掘时间 $ x $(天)之间的关系如图所示。
(1) 甲组比乙组多挖掘了30天。
(2) 求乙组停工后,$ y $ 关于 $ x $ 的函数表达式,并写出自变量 $ x $ 的取值范围。
(3) 当甲组挖掘的总长度与乙组挖掘的总长度相等时,直接写出乙组已停工的天数。

答案： 3.解:
(1)30
(2)设乙组停工后,y关于x的函数表达式为y=kx+b.
∵点(30,210),(60,300)在图象上,
∴{30k+b=210,60k+b=300,解得{k=3,b=120,
∴y关于x的函数表达式为y=3x+120(30≤x≤60).
(3)10天.

4. 甲、乙两个工程队分别同时开挖两段河渠,所挖河渠的长度 $ y $(m)与挖掘时间 $ x $(h)之间的函数关系如图所示。请根据图象提供的信息,解答下列问题：
(1) 甲队在开挖后 6 h 内,每小时挖10m。
(2) 当 $ 2 \leq x \leq 6 $ 时,求 $ y_{乙} $ 与 $ x $ 之间的函数关系式。
(3) 直接写出开挖后几小时,甲、乙两队挖的河渠的长度相差 5 m。

答案： 4.解:
(1)10
(2)设当2≤x≤6时,y乙与x之间的关系式为y乙=kx+b(k≠0).
∵函数图象过点(2,30),(6,50),
∴{2k+b=30,6k+b=50,解得{k=5,b=20,
∴当2≤x≤6时,y乙与x之间的关系式为y乙=5x+20.
(3)开挖后1h或3h或5h,甲、乙两队挖的河渠的长度相差5m.