第63页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
9. 新考向 跨学科 电子体重秤原理是利用力传感器在置物平台上放上重物后,使表面发生形变而引发了内置电阻的形状变化,电阻的形变必然引发电阻值的变化,电阻值的变化又使内部电流发生变化产生了相应的电信号,电信号经过处理后就成了可视数字。简易电子秤制作方法:制作一个装有踏板(踏板质量忽略不计)的可变电阻$R_1,$已知$R_1$与踏板上人的质量m之间的关系式为$R_1= km+b($其中k,b为常数,0≤m≤120),如图所示。下列说法不正确的是(
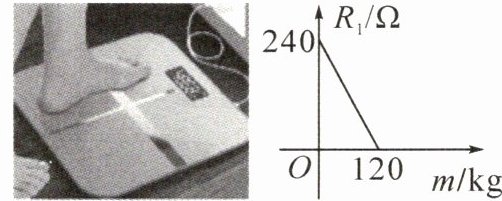
A.b= 240
B.可变电阻$R_1$随着踏板上人的质量m的增加而减小
C.当踏板上人的质量m每增加10kg,可变电阻$R_1$减小20Ω
D.当可变电阻$R_1$为90Ω时,对应测得人的质量m为60kg
D
)
A.b= 240
B.可变电阻$R_1$随着踏板上人的质量m的增加而减小
C.当踏板上人的质量m每增加10kg,可变电阻$R_1$减小20Ω
D.当可变电阻$R_1$为90Ω时,对应测得人的质量m为60kg
答案:
D
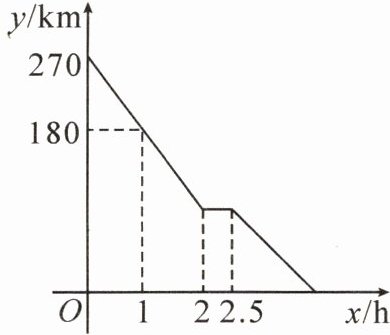
10. 小蕾家与外婆家相距270km,她假期去看望外婆,返回时,恰好有一辆顺风车可以带小蕾到A服务区,于是,小蕾与爸爸约定,她先搭乘顺风车到A服务区,爸爸驾车到A服务区接小蕾回家。两人在A服务区见面后,休息了一会儿,然后小蕾乘坐爸爸的车以60km/h的速度返回家中。在小蕾的整个行程中,小蕾与自己家的距离y(km)和时间x(h)之间的关系如图所示。
(1)求小蕾从外婆家到A服务区的过程中,y与x之间的关系式。
(2)小蕾从外婆家回到自己家共用了多长时间?
]
(1)求小蕾从外婆家到A服务区的过程中,y与x之间的关系式。
(2)小蕾从外婆家回到自己家共用了多长时间?
]

答案:
解:
(1)设$ y $与$ x $之间的关系式为$ y=kx+b $.根据题意,得$ 270=b $,① $ 180=k+b $.② 将①代入②,得$ k=-90 $.$ \therefore y=-90x+270(0\leqslant x\leqslant 2) $.
(2)把$ x=2 $代入$ y=-90x+270 $,得$ y=90 $.从A服务区到家的时间为$ 90÷ 60=1.5(h) $.$ \therefore 2.5+1.5=4(h) $.答:小蕾从外婆家回到自己家共用了4h.
(1)设$ y $与$ x $之间的关系式为$ y=kx+b $.根据题意,得$ 270=b $,① $ 180=k+b $.② 将①代入②,得$ k=-90 $.$ \therefore y=-90x+270(0\leqslant x\leqslant 2) $.
(2)把$ x=2 $代入$ y=-90x+270 $,得$ y=90 $.从A服务区到家的时间为$ 90÷ 60=1.5(h) $.$ \therefore 2.5+1.5=4(h) $.答:小蕾从外婆家回到自己家共用了4h.
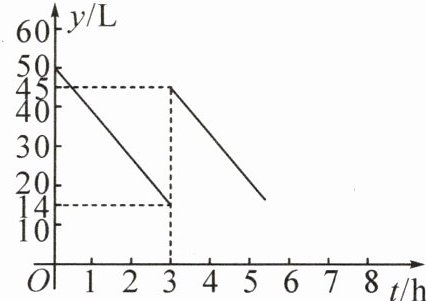
11. 已知汽车出发前油箱有油50L,行驶若干小时后,在加油站加油若干升。汽车从出发后,油箱中剩余油量y(L)与行驶时间t(h)之间的关系如图所示。
(1)汽车行驶
(2)写出加油前油箱剩余油量y与行驶时间t之间的关系式y= kt+b,其中k和b的实际意义分别是什么?
(3)已知加油前、后汽车都以70km/h的速度匀速行驶,如果加油站距目的地280km,那么要到达目的地,油箱中的油是否够用?请说明理由。
]
(1)汽车行驶
3
h后加油,中途加油______31
L。(2)写出加油前油箱剩余油量y与行驶时间t之间的关系式y= kt+b,其中k和b的实际意义分别是什么?
(3)已知加油前、后汽车都以70km/h的速度匀速行驶,如果加油站距目的地280km,那么要到达目的地,油箱中的油是否够用?请说明理由。
]

答案:
解:
(1)3 31
(2)根据题意,得$ 50=b $,①$ 14=3k+b $.②将①代入②,得$ k=-12 $.$ \therefore $加油前$ y $与$ t $之间的关系式为$ y=-12t+50(0\leqslant t\leqslant 3) $.$ k $表示每小时汽车的耗油量,$ b $表示出发前油箱的油量.
(3)要到达目的地,油箱中的油不够用.理由如下:$ 280÷ 70=4(h) $,$ 12× 4=48(L) $,$ \because 45<48 $,$ \therefore $要到达目的地,油箱中的油不够用.
(1)3 31
(2)根据题意,得$ 50=b $,①$ 14=3k+b $.②将①代入②,得$ k=-12 $.$ \therefore $加油前$ y $与$ t $之间的关系式为$ y=-12t+50(0\leqslant t\leqslant 3) $.$ k $表示每小时汽车的耗油量,$ b $表示出发前油箱的油量.
(3)要到达目的地,油箱中的油不够用.理由如下:$ 280÷ 70=4(h) $,$ 12× 4=48(L) $,$ \because 45<48 $,$ \therefore $要到达目的地,油箱中的油不够用.
12. 小李和小王分别从甲、乙两地同时步行出发,匀速相向而行。小李的速度大于小王的速度,小李到达乙地后,小王继续前行。设出发x h后,两人相距y km,如图所示,折线表示从两人出发至小王到达甲地的过程中y与x之间的函数关系。下列说法错误的是(
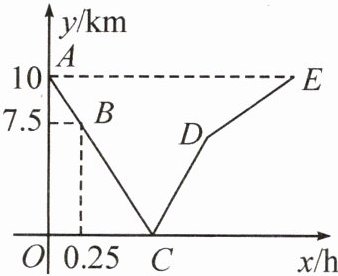
A.点A的坐标意义是甲、乙两地相距10km
B.由点B可知,出发0.25h,小李、小王共走了2.5km
C.点C表示小李、小王相遇,点C的横坐标为0.75
D.线段DE表示小李到达乙地后,小王步行至甲地的运动过程
]
C
)
A.点A的坐标意义是甲、乙两地相距10km
B.由点B可知,出发0.25h,小李、小王共走了2.5km
C.点C表示小李、小王相遇,点C的横坐标为0.75
D.线段DE表示小李到达乙地后,小王步行至甲地的运动过程
]
答案:
C
查看更多完整答案,请扫码查看


