第26页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
1. 计算$\sqrt{27}-\sqrt{8}×\sqrt{\frac{3}{2}}$的结果是(
A.$\sqrt{3}$
B.$-\sqrt{3}$
C.$2\sqrt{3}$
D.$5\sqrt{3}$
A
)A.$\sqrt{3}$
B.$-\sqrt{3}$
C.$2\sqrt{3}$
D.$5\sqrt{3}$
答案:
A
2. 老师设计了一个“接力游戏”,让同学们用合作的方式完成二次根式的混合运算.如图,老师把题目交给一位同学,他完成一步解答后交给第二位同学,依次进行,最后完成运算.规则是每人只能看到前一人传过来的式子.接力中,自己负责的运算出现错误的是(
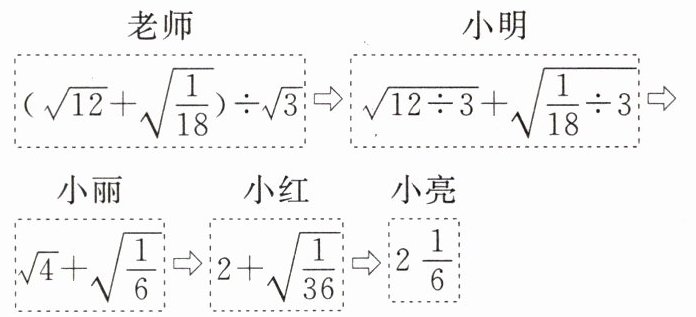
A.小明和小丽
B.小丽和小红
C.小红和小亮
D.小丽和小亮
B
)
A.小明和小丽
B.小丽和小红
C.小红和小亮
D.小丽和小亮
答案:
B
3. 若$a + b = 3$,$ab = 1$,则式子$\sqrt{\frac{a}{b}}+\sqrt{\frac{b}{a}}$的值为(
A.3
B.$-3$
C.$\sqrt{3}$
D.$-\sqrt{3}$
A
)A.3
B.$-3$
C.$\sqrt{3}$
D.$-\sqrt{3}$
答案:
A
4. 在$(\sqrt{27}+\sqrt{\frac{1}{3}})□\sqrt{3}的□$中添加一个运算符号,使其结果最大,则$□$中应添加(
A.$+$
B.$-$
C.$×$
D.$÷$
C
)A.$+$
B.$-$
C.$×$
D.$÷$
答案:
C
5. 计算:
(1) $\sqrt{24}-\sqrt{\frac{6}{5}}×\sqrt{45}=$
(2) $(-\sqrt{12}+\sqrt{\frac{1}{3}})÷\sqrt{27}=$
(1) $\sqrt{24}-\sqrt{\frac{6}{5}}×\sqrt{45}=$
$-\sqrt{6}$
.(2) $(-\sqrt{12}+\sqrt{\frac{1}{3}})÷\sqrt{27}=$
$-\dfrac{5}{9}$
.
答案:
(1)$-\sqrt{6}$
(2)$-\dfrac{5}{9}$
(1)$-\sqrt{6}$
(2)$-\dfrac{5}{9}$
6. 计算:
(1) $\sqrt{\frac{2}{5}}-\sqrt{\frac{5}{2}}$.
(2) $\sqrt{80}-\sqrt{20}+\sqrt{\frac{1}{5}}$.
(3) $\frac{\sqrt{50}×\sqrt{32}}{\sqrt{8}}-\sqrt[3]{-8}$.
(4) $\sqrt{12}÷(\frac{\sqrt{3}}{4}+\frac{2\sqrt{3}}{3})$.
(1) $\sqrt{\frac{2}{5}}-\sqrt{\frac{5}{2}}$.
(2) $\sqrt{80}-\sqrt{20}+\sqrt{\frac{1}{5}}$.
(3) $\frac{\sqrt{50}×\sqrt{32}}{\sqrt{8}}-\sqrt[3]{-8}$.
(4) $\sqrt{12}÷(\frac{\sqrt{3}}{4}+\frac{2\sqrt{3}}{3})$.
答案:
解:
(1)原式$=\dfrac{\sqrt{10}}{5}-\dfrac{\sqrt{10}}{2}=-\dfrac{3\sqrt{10}}{10}$.
(2)原式$=4\sqrt{5}-2\sqrt{5}+\dfrac{\sqrt{5}}{5}=2\sqrt{5}+\dfrac{1}{5}\sqrt{5}=\dfrac{11}{5}\sqrt{5}$.
(3)原式$=\dfrac{5\sqrt{2}× 4\sqrt{2}}{2\sqrt{2}}-(-2)=10\sqrt{2}+2$.
(4)原式$=\sqrt{12}÷ \left(\dfrac{3\sqrt{3}}{12}+\dfrac{8\sqrt{3}}{12}\right)=\sqrt{12}÷ \dfrac{11\sqrt{3}}{12}=2\sqrt{3}× \dfrac{12}{11\sqrt{3}}=\dfrac{24}{11}$.
(1)原式$=\dfrac{\sqrt{10}}{5}-\dfrac{\sqrt{10}}{2}=-\dfrac{3\sqrt{10}}{10}$.
(2)原式$=4\sqrt{5}-2\sqrt{5}+\dfrac{\sqrt{5}}{5}=2\sqrt{5}+\dfrac{1}{5}\sqrt{5}=\dfrac{11}{5}\sqrt{5}$.
(3)原式$=\dfrac{5\sqrt{2}× 4\sqrt{2}}{2\sqrt{2}}-(-2)=10\sqrt{2}+2$.
(4)原式$=\sqrt{12}÷ \left(\dfrac{3\sqrt{3}}{12}+\dfrac{8\sqrt{3}}{12}\right)=\sqrt{12}÷ \dfrac{11\sqrt{3}}{12}=2\sqrt{3}× \dfrac{12}{11\sqrt{3}}=\dfrac{24}{11}$.
7. 在计算$(\sqrt{24}-\sqrt{\frac{1}{2}})-(\sqrt{\frac{1}{8}}+\sqrt{6})$时,小敏的解题过程如下:
解:原式$=(2\sqrt{6}-\frac{\sqrt{2}}{2})-(\frac{\sqrt{2}}{4}+\sqrt{6})…$①
$=2\sqrt{6}-\frac{\sqrt{2}}{2}-\frac{\sqrt{2}}{4}+\sqrt{6}…$②
$=2\sqrt{6}+\sqrt{6}-\frac{\sqrt{2}}{2}-\frac{\sqrt{2}}{4}…$③
$=3\sqrt{6}-\frac{\sqrt{2}}{4}…$④
(1) 老师判定小敏的解题过程错误,请指出小敏是从第______步开始出错的.(填序号)
(2) 请写出正确的解题过程.
(1)
(2)
解:原式$=(2\sqrt{6}-\frac{\sqrt{2}}{2})-(\frac{\sqrt{2}}{4}+\sqrt{6})…$①
$=2\sqrt{6}-\frac{\sqrt{2}}{2}-\frac{\sqrt{2}}{4}+\sqrt{6}…$②
$=2\sqrt{6}+\sqrt{6}-\frac{\sqrt{2}}{2}-\frac{\sqrt{2}}{4}…$③
$=3\sqrt{6}-\frac{\sqrt{2}}{4}…$④
(1) 老师判定小敏的解题过程错误,请指出小敏是从第______步开始出错的.(填序号)
(2) 请写出正确的解题过程.
(1)
②
(2)
解:原式$=(2\sqrt{6}-\frac{\sqrt{2}}{2})-(\frac{\sqrt{2}}{4}+\sqrt{6})=2\sqrt{6}-\frac{\sqrt{2}}{2}-\frac{\sqrt{2}}{4}-\sqrt{6}=2\sqrt{6}-\sqrt{6}-(\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{4})=\sqrt{6}-\frac{3\sqrt{2}}{4}$
答案:
解:
(1)②
(2)原式$=\left(2\sqrt{6}-\dfrac{\sqrt{2}}{2}\right)-\left(\dfrac{\sqrt{2}}{4}+\sqrt{6}\right)=2\sqrt{6}-\dfrac{\sqrt{2}}{2}-\dfrac{\sqrt{2}}{4}-\sqrt{6}=2\sqrt{6}-\sqrt{6}-\left(\dfrac{\sqrt{2}}{2}+\dfrac{\sqrt{2}}{4}\right)=\sqrt{6}-\dfrac{3\sqrt{2}}{4}$.
(1)②
(2)原式$=\left(2\sqrt{6}-\dfrac{\sqrt{2}}{2}\right)-\left(\dfrac{\sqrt{2}}{4}+\sqrt{6}\right)=2\sqrt{6}-\dfrac{\sqrt{2}}{2}-\dfrac{\sqrt{2}}{4}-\sqrt{6}=2\sqrt{6}-\sqrt{6}-\left(\dfrac{\sqrt{2}}{2}+\dfrac{\sqrt{2}}{4}\right)=\sqrt{6}-\dfrac{3\sqrt{2}}{4}$.
查看更多完整答案,请扫码查看


