第111页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
1. (1) 问题发现:如图 1,直线 $ AB // CD $,连接 $ BE $,$ CE $,可以发现 $ \angle BEC = \angle B + \angle C $。
请把下面的证明过程补充完整:
证明:过点 $ E $ 作 $ EF // AB $。
$ \therefore \angle B = \angle BEF $(
$ \because AB // CD $(已知),
$ \therefore EF // CD $(
$ \therefore \angle C = \angle CEF $。
$ \therefore \angle BEF + \angle CEF = \angle B + $
$ \therefore \angle BEC = \angle B + \angle C $(等量代换)。
(2) 拓展探究:如果点 $ E $ 运动到如图 2 所示的位置,其他条件不变。求证:$ \angle B + \angle C + \angle BEC = 360^{\circ} $。

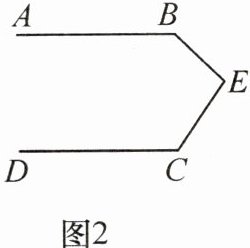
请把下面的证明过程补充完整:
证明:过点 $ E $ 作 $ EF // AB $。
$ \therefore \angle B = \angle BEF $(
两直线平行,内错角相等
)。$ \because AB // CD $(已知),
$ \therefore EF // CD $(
平行于同一条直线的两条直线平行
)。$ \therefore \angle C = \angle CEF $。
$ \therefore \angle BEF + \angle CEF = \angle B + $
$ \angle C $
。$ \therefore \angle BEC = \angle B + \angle C $(等量代换)。
(2) 拓展探究:如果点 $ E $ 运动到如图 2 所示的位置,其他条件不变。求证:$ \angle B + \angle C + \angle BEC = 360^{\circ} $。


答案:
1.(1)两直线平行,内错角相等 平行于同一条直线的两条直线平行 ∠C (2)证明:过点 E 作 EF//AB(点 F 在点 E 左侧).
∴∠B+∠BEF=180°.
∵AB//CD,
∴EF//CD.
∴∠C+∠CEF=180°.
∴∠B+∠BEF+∠C+∠CEF=360°.
∴∠B+∠C+∠BEC=360°.
∴∠B+∠BEF=180°.
∵AB//CD,
∴EF//CD.
∴∠C+∠CEF=180°.
∴∠B+∠BEF+∠C+∠CEF=360°.
∴∠B+∠C+∠BEC=360°.
【拓展变式】 如图,$ AB // CD $,$ \angle BED = 110^{\circ} $,$ BF $ 平分 $ \angle ABE $,$ DF $ 平分 $ \angle CDE $,则 $ \angle BFD = $______。
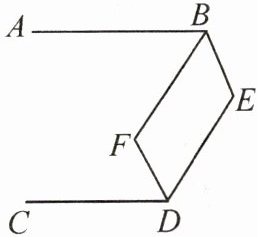

答案:
【拓展变式】 125°
2. 已知 $ AB // CD $,$ E $ 为 $ AB $,$ CD $ 之外任意一点。
(1) 如图 1,探究 $ \angle BED $ 与 $ \angle B $,$ \angle D $ 之间的数量关系,并说明理由。

(2) 如图 2,探究 $ \angle CDE $ 与 $ \angle B $,$ \angle BED $ 之间的数量关系,并说明理由。

2.解:
(1)∠B=∠BED+∠D.理由:过点 E 作 EF//AB(点 F 在点 E 右侧),则 AB//CD//EF.
∴∠BEF=∠B,∠D=∠DEF.
∵∠BEF=∠BED+∠DEF,
∴∠B=∠BED+∠D.
(2)∠CDE=∠B+∠BED.理由:过点 E 作 EF//AB(点 F 在点 E 右侧),则 AB//CD//EF.
∴∠B=∠BEF,∠CDE=∠DEF.
∵∠DEF=∠BEF+∠BED,
∴∠CDE=∠B+∠BED.
(1) 如图 1,探究 $ \angle BED $ 与 $ \angle B $,$ \angle D $ 之间的数量关系,并说明理由。

(2) 如图 2,探究 $ \angle CDE $ 与 $ \angle B $,$ \angle BED $ 之间的数量关系,并说明理由。

2.解:
(1)∠B=∠BED+∠D.理由:过点 E 作 EF//AB(点 F 在点 E 右侧),则 AB//CD//EF.
∴∠BEF=∠B,∠D=∠DEF.
∵∠BEF=∠BED+∠DEF,
∴∠B=∠BED+∠D.
(2)∠CDE=∠B+∠BED.理由:过点 E 作 EF//AB(点 F 在点 E 右侧),则 AB//CD//EF.
∴∠B=∠BEF,∠CDE=∠DEF.
∵∠DEF=∠BEF+∠BED,
∴∠CDE=∠B+∠BED.
答案:
2.解:
(1)∠B=∠BED+∠D.理由:过点 E 作 EF//AB(点 F 在点 E 右侧),则 AB//CD//EF.
∴∠BEF=∠B,∠D=∠DEF.
∵∠BEF=∠BED+∠DEF,
∴∠B=∠BED+∠D.
(2)∠CDE=∠B+∠BED.理由:过点 E 作 EF//AB(点 F 在点 E 右侧),则 AB//CD//EF.
∴∠B=∠BEF,∠CDE=∠DEF.
∵∠DEF=∠BEF+∠BED,
∴∠CDE=∠B+∠BED.
(1)∠B=∠BED+∠D.理由:过点 E 作 EF//AB(点 F 在点 E 右侧),则 AB//CD//EF.
∴∠BEF=∠B,∠D=∠DEF.
∵∠BEF=∠BED+∠DEF,
∴∠B=∠BED+∠D.
(2)∠CDE=∠B+∠BED.理由:过点 E 作 EF//AB(点 F 在点 E 右侧),则 AB//CD//EF.
∴∠B=∠BEF,∠CDE=∠DEF.
∵∠DEF=∠BEF+∠BED,
∴∠CDE=∠B+∠BED.
【拓展变式】 新考向 传统文化 如图,“抖空竹”是国家级非物质文化遗产。在“抖空竹”的一个瞬间如图 1 所示,将图 1 抽象成一个数学问题:如图 2,若 $ AB // CD $,$ \angle EAB = 70^{\circ} $,$ \angle ECD = 110^{\circ} $,则 $ \angle E = $______。




答案:
【拓展变式】 40°
3. 如图,$ AB // EF $,$ BC \perp CD $,则 $ \angle \alpha $,$ \angle \beta $,$ \angle \gamma $ 之间的关系是(

A.$ \angle \beta = \angle \alpha + \angle \gamma $
B.$ \angle \alpha + \angle \beta + \angle \gamma = 180^{\circ} $
C.$ \angle \alpha + \angle \beta - \angle \gamma = 90^{\circ} $
D.$ \angle \beta + \angle \gamma - \angle \alpha = 90^{\circ} $
C
)
A.$ \angle \beta = \angle \alpha + \angle \gamma $
B.$ \angle \alpha + \angle \beta + \angle \gamma = 180^{\circ} $
C.$ \angle \alpha + \angle \beta - \angle \gamma = 90^{\circ} $
D.$ \angle \beta + \angle \gamma - \angle \alpha = 90^{\circ} $
答案:
3.C
4. 观察图形:
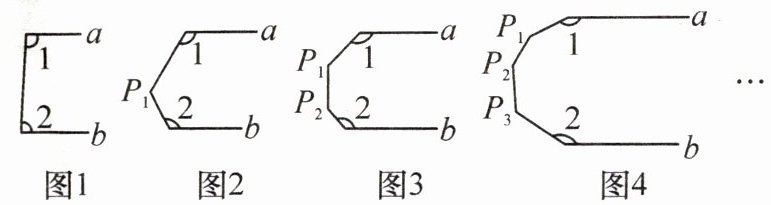
已知 $ a // b $,在图 1 中,可得 $ \angle 1 + \angle 2 = $

已知 $ a // b $,在图 1 中,可得 $ \angle 1 + \angle 2 = $
180
$^{\circ}$,在图 2 中,可得 $ \angle 1 + \angle 2 + \angle P_1 = $360
$^{\circ}$……按照以上规律,则 $ \angle 1 + \angle 2 + \angle P_1 + … + \angle P_n = $180(n+1)
$^{\circ}$。
答案:
4.180 360 180(n+1)
查看更多完整答案,请扫码查看


