第9页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
8. 如图,这是由7个大小相同的小正方体堆砌而成的几何体.若从标有①②③④的四个小正方体中取走一个后,余下几何体与原几何体的从正面看到的形状图相同,则取走的正方体是(

A.①
B.②
C.③
D.④
A
)
A.①
B.②
C.③
D.④
答案:
A
9. 用4个相同的小正方体搭几何体,要求每个几何体从正面、左面、上面看到的形状图中至少有两种是相同的,则下列四种摆放方式中不符合要求的是(

D
)
答案:
D
10. 从正面、左面、上面观察一个由小正方体构成的几何体依次得到以下的形状图,则构成这个几何体的小正方体有(

A.4个
B.5个
C.6个
D.7个
B
)
A.4个
B.5个
C.6个
D.7个
答案:
B
11.(教材P17习题T8变式)一个小正方体的六个面分别标有字母A,B,C,D,E,F,从三个不同方向看到的情形如图所示,则C,A,E相对面的字母分别是(
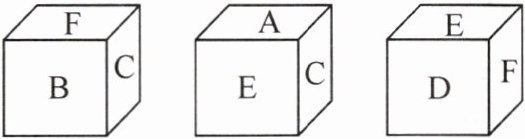
A.D,F,B
B.D,B,F
C.B,F,D
D.B,D,F
A
)
A.D,F,B
B.D,B,F
C.B,F,D
D.B,D,F
答案:
A
12. 由一些大小相同的小正方体搭成的简单几何体从正面和上面看到的形状图如图所示:

(1)请画出这个几何体的一种从左面看到的形状图.
(2)若组成这个几何体的小正方体的个数为n,请你写出n的所有可能值.

(1)请画出这个几何体的一种从左面看到的形状图.
(2)若组成这个几何体的小正方体的个数为n,请你写出n的所有可能值.
答案:
解:
(1)答案不唯一,图略.
(2)$n=8,9,10,11$.
(1)答案不唯一,图略.
(2)$n=8,9,10,11$.
13. 如图,在平整的地面上,用多个棱长都为2cm的小正方体堆成一个几何体.
(1)共有____个小正方体.
(2)若在几何体表面(露出部分,不含底面)喷漆,求这个几何体喷漆的面积.
(3)如果现在你还有一些棱长都为2cm的小正方体,要求保持从上面看和从左面看的形状图都不变,最多可以再添加____个小正方体.
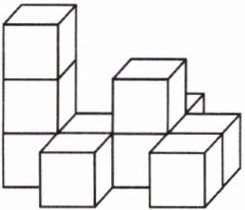
(1)共有____个小正方体.
(2)若在几何体表面(露出部分,不含底面)喷漆,求这个几何体喷漆的面积.
(3)如果现在你还有一些棱长都为2cm的小正方体,要求保持从上面看和从左面看的形状图都不变,最多可以再添加____个小正方体.

答案:
解:
(1)10
(2)这个几何体从正面看得到的形状图的面积为$2×2×7=28(cm^2)$,从左面看得到的形状图的面积为$2×2×5=20(cm^2)$,从上面看得到的形状图的面积为$2×2×7=28(cm^2)$,$\therefore$该几何体喷漆的面积为$28×2+20×2+28+4×2×2=140(cm^2)$.
(3)5 [解法提示]从上面看几何体得到的形状图如图所示,小正方形上的数字表示最多添加小正方体的个数,使其从上面看和从左面看得到的形状图都不变.$\therefore$最多可以添加5个小正方体.

解:
(1)10
(2)这个几何体从正面看得到的形状图的面积为$2×2×7=28(cm^2)$,从左面看得到的形状图的面积为$2×2×5=20(cm^2)$,从上面看得到的形状图的面积为$2×2×7=28(cm^2)$,$\therefore$该几何体喷漆的面积为$28×2+20×2+28+4×2×2=140(cm^2)$.
(3)5 [解法提示]从上面看几何体得到的形状图如图所示,小正方形上的数字表示最多添加小正方体的个数,使其从上面看和从左面看得到的形状图都不变.$\therefore$最多可以添加5个小正方体.

查看更多完整答案,请扫码查看


