《2025年同步精练广东七年级数学上册北师大版》

1. 有一种游戏的规则如下：你任想一个数,将这个数乘 3,加上 9,除以 3,最后减去你所想的数,我就知道结果,那么结果是(C)
A.1
B.2
C.3
D.4

答案： C

2.(教材 P99 习题 T3 变式)小明和小亮做猜数字游戏,小明对小亮说：“你心里想好一个两位数,将十位数字乘 2,然后加 3,再将所得新数乘 5,最后将得到的数加上个位数字,计算出结果。”小亮计算后说得到的是 37,小明立刻说出了小亮心里想的两位数是22。

答案： 22

3. 一个数学游戏的步骤如下：
第一步：取一个自然数 $ x_{1}= 5 $,计算 $ x_{1}^{2}+1 $ 得 $ y_{1} $；
第二步：算出 $ y_{1} $ 的各数位上的数字之和得 $ x_{2} $,计算 $ x_{2}^{2}+1 $ 得 $ y_{2} $；
第三步：算出 $ y_{2} $ 的各数位上的数字之和得 $ x_{3} $,计算 $ x_{3}^{2}+1 $ 得 $ y_{3} $；
……
依此类推,则 $ y_{30}= $122。

答案： 122

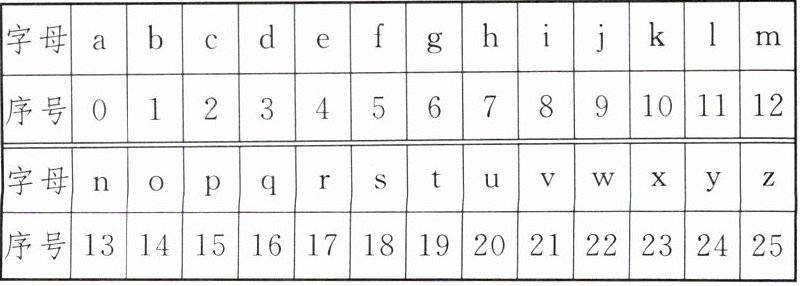
4.(教材 P99 习题 T4 变式)有一种密码,将 26 个英文字母 a,b,c,…,z 不论大小写依次对应 0,1,2,3,…,25 这 26 个自然数(如表格),当明码对应的序号 $ x $ 为奇数时,密码对应的序号为 $ \frac{|x - 33|}{2} $；当明码对应的序号 $ x $ 为偶数时,密码对应的序号为 $ \frac{x}{2}+5 $。按上述规定,将明码“efuz”译成密码是hope。

答案： hope

5. 小明在研究数学问题时发现一个有趣的现象：

请用不同的三位数再做一做,你会发现什么有趣的现象？用学过的知识解释。

答案： 解:举例不唯一,如:614-416=198,198+891=1089. 发现:结果一定是1089. 设百位数字为a(2＜a≤9,且a为整数),十位数字为b,则个位数字为a-2.
∴该三位数为100a+10b+a-2=101a+10b-2,交换百位数字与个位数字后的三位数为100(a-2)+10b+a=101a+10b-200.
∴101a+10b-2-(101a+10b-200)=198.
∴198+891=1089.
∴结果一定是1089.

6. 新考向 代数推理 若一个三位数的百位数字与个位数字的和是十位数字的 2 倍,则称这个三位数是“团结数”。例如：对于三位数 246,它的百位数字为 2,个位数字为 6,十位数字为 4,满足 $ 2 + 6 = 4×2 $,则 246 是“团结数”。
(1)任写一个小于 200 的“团结数”：111(答案不唯一)。
(2)请说明任意一个“团结数”一定是 3 的倍数。

答案：
(1)111(答案不唯一)
(2)设"团结数"的百位数字为a,个位数字为c,十位数字为b,则这个"团结数"可以表示为100a+10b+c.
∵a+c=2b,
∴100a+10b+c=(99+1)a+(9+1)b+c=99a+9b+(a+b+c)=99a+9b+(2b+b)=99a+9b+3b=99a+12b. 其中99a肯定是3的倍数,12b也是3的倍数.
∴任意一个"团结数"一定是3的倍数.