《2025年同步精练广东七年级数学上册北师大版》

1. 小亮在做“计算$(5x^{3}+2x^{4}y-3xy^{2})+(x^{3}+3xy^{2}+y^{3})-(6x^{3}-x^{2}y^{2}+2y^{2})$的值,其中$x= 2,y= -1$”这道题时,把“$x= 2$”错看成“$x= -2$”,但他计算的结果却是正确的. 请说明其原因.

答案： 解:原式=5x³+2x⁴y-3xy²+x³+3xy²+y³-6x³+x²y²-2y³=2x⁴y+y³+x²y²-2y³.
∵化简结果中只含有x的偶次项,且2和-2互为相反数,
∴x=2和x=-2的计算结果相同,
∴他计算的结果也是正确的.

2. 在学习了整式的加减后,老师给出一道课堂练习题：
选择$a$的一个值,求$5a^{3}-(a^{2}-3a+3a^{3})+(a^{2}-a-2a^{3})-2a+2035$的值.
甲说：“当$a= 0$时,原式$=2035$.”
乙说：“当$a= 1$时,原式$=2035$.”
丙说：“当$a$为任何一个有理数时,原式$=2035$.”
这三位同学的说法是否正确？请说明理由.

答案： 解:这三位同学的说法正确.理由如下:原式=5a³-a²+3a-3a³+a²-a-2a³-2a+2035=2035,故这三位同学的说法正确.

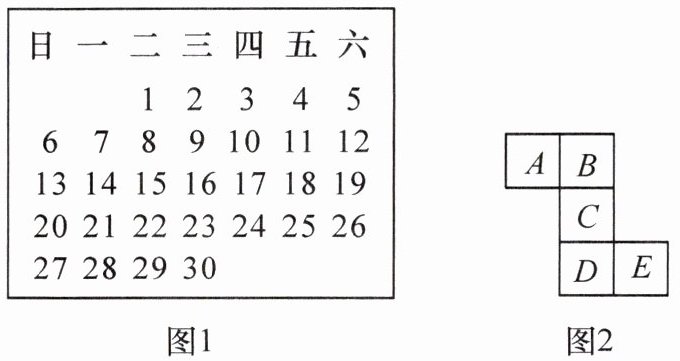
3. 如图1,这是某年11月的月历,用如图2所示的“Z”字形覆盖住月历中的五个数,这五个数从小到大依次为$A,B,C,D,E$. 则这五个数的和能被5整除吗？为什么？
(1) 甲同学设$A= x$,请通过计算得出结论.
(2) 乙同学说自己设$C= x$更简单,请你也来试一试.
(3) 小明受到启发,改编了下面一道题目,请解答：
代数式$A-2B+3C+4D-6E$的值是否为定值？若是,请求出它的值；若不是,请说明理由.

答案：
(1)设A=x,则B=x+1,C=x+8,D=x+15,E=x+16.
∴A+B+C+D+E=x+x+1+x+8+x+15+x+16=5x+40=5(x+8).
∵5(x+8)是5的倍数,
∴5(x+8)能被5整除.
∴这五个数的和能被5整除.
(2)设C=x,则D=x+7,E=x+8,B=x-7,A=x-8.
∴A+B+C+D+E=x-8+x-7+x+x+7+x+8=5x.
∵5x能被5整除,
∴这五个数的和能被5整除.
(3)设C=x,则D=x+7,E=x+8,B=x-7,A=x-8.
∴A-2B+3C+4D-6E=x-8-2(x-7)+3x+4(x+7)-6(x+8)=x-8-2x+14+3x+4x+28-6x-48=-14.
∴代数式A-2B+3C+4D-6E的值是定值,为-14.