第103页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
6. 某校举办体操表演,七年级(1)班在排练过程中因有2人请假需要重新排列队形,原来每排7人,重新排列队形之后,每排9人,这样比原来减少了2排,则原来有(
A.6排
B.7排
C.8排
D.9排
C
)A.6排
B.7排
C.8排
D.9排
答案:
C
7. 新考向 数学文化我国古代数学著作《孙子算经》中有这样一道题,原文如下:今有百鹿入城,家取一鹿,不尽,又三家共一鹿,适尽,问城中家几何?大意为:今有100头鹿进城,每家取一头鹿,没有取完,剩下的鹿每3家共取一头,恰好取完,问:城中有多少户人家?在这个问题中,城中人家的户数为(
A.25
B.75
C.81
D.90
B
)A.25
B.75
C.81
D.90
答案:
B
8. 小乐和小丽所在的社团活动小组计划做一批“贺卡”,如果每人做8个,那么比计划多了6个;如果每人做5个,那么比计划少30个,则该小组共有多少人?计划做多少个“贺卡”?
她俩经过独立思考后,分别列出了如下尚不完整的方程:
小乐的方法:$8x□(\quad)= 5x□(\quad)$;
小丽的方法:$\frac{y□(\quad)}{8}= \frac{y□(\quad)}{5}$.
(1)在小乐、小丽所列的方程中,“$□$”中是运算符号,“$(\quad)$”中是数,请根据她们所列的方程分别指出未知数$x$,$y$表示的意义.
(2)选择一种方法,将原题中的问题解答完整.
(1)由题意知,$x$表示该小组人数,$y$表示活动小组计划做的"贺卡"数.
(2)答案不唯一,选择小乐的方法:设该小组有$x$人.由题意,得$8x-6=5x+30$,解得$x=12$.计划做的"贺卡"有$8×12-6=90$(个).答:该小组共有12人,计划做的"贺卡"有90个.
她俩经过独立思考后,分别列出了如下尚不完整的方程:
小乐的方法:$8x□(\quad)= 5x□(\quad)$;
小丽的方法:$\frac{y□(\quad)}{8}= \frac{y□(\quad)}{5}$.
(1)在小乐、小丽所列的方程中,“$□$”中是运算符号,“$(\quad)$”中是数,请根据她们所列的方程分别指出未知数$x$,$y$表示的意义.
(2)选择一种方法,将原题中的问题解答完整.
(1)由题意知,$x$表示该小组人数,$y$表示活动小组计划做的"贺卡"数.
(2)答案不唯一,选择小乐的方法:设该小组有$x$人.由题意,得$8x-6=5x+30$,解得$x=12$.计划做的"贺卡"有$8×12-6=90$(个).答:该小组共有12人,计划做的"贺卡"有90个.
答案:
解:
(1)由题意知,$x$表示该小组人数,$y$表示活动小组计划做的"贺卡"数.
(2)答案不唯一,选择小乐的方法:设该小组有$x$人.由题意,得$8x-6=5x+30$,解得$x=12$.计划做的"贺卡"有$8×12-6=90$(个).答:该小组共有12人,计划做的"贺卡"有90个.
(1)由题意知,$x$表示该小组人数,$y$表示活动小组计划做的"贺卡"数.
(2)答案不唯一,选择小乐的方法:设该小组有$x$人.由题意,得$8x-6=5x+30$,解得$x=12$.计划做的"贺卡"有$8×12-6=90$(个).答:该小组共有12人,计划做的"贺卡"有90个.
9. 某企业采购了A品牌冰箱40台,B品牌冰箱60台,准备让旗下的甲、乙两家商场卖出,其中70台给甲商场,30台给乙商场.设企业调配给甲商场$x$($x$为正整数)台A品牌冰箱.两家商场销售这两种品牌冰箱每台的利润如下表(单位:元):
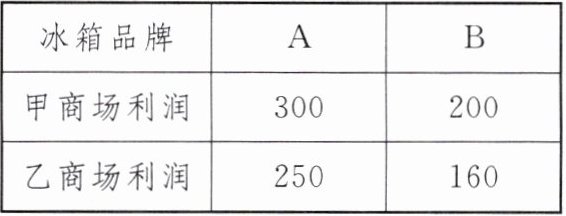
(1)请根据题意补全A,B品牌冰箱调配情况的表格(单位:台):
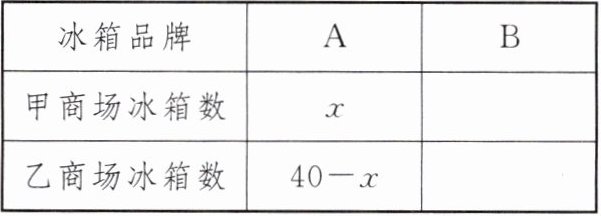
(2)若甲、乙两家商场全部卖出这100台冰箱的总利润为22700元,求$x$的值.
(3)为了促销,企业决定仅对甲商场的A品牌冰箱每台降价$a$元销售,甲商场的B品牌冰箱以及乙商场的A,B品牌冰箱的销售利润都不变.若无论甲商场销售A品牌冰箱多少台,这100台冰箱全部售完后企业总利润保持不变,求$a$的值.
(1)请根据题意补全A,B品牌冰箱调配情况的表格(单位:台):
(2)若甲、乙两家商场全部卖出这100台冰箱的总利润为22700元,求$x$的值.
(3)为了促销,企业决定仅对甲商场的A品牌冰箱每台降价$a$元销售,甲商场的B品牌冰箱以及乙商场的A,B品牌冰箱的销售利润都不变.若无论甲商场销售A品牌冰箱多少台,这100台冰箱全部售完后企业总利润保持不变,求$a$的值.

(1)请根据题意补全A,B品牌冰箱调配情况的表格(单位:台):

(2)若甲、乙两家商场全部卖出这100台冰箱的总利润为22700元,求$x$的值.
(3)为了促销,企业决定仅对甲商场的A品牌冰箱每台降价$a$元销售,甲商场的B品牌冰箱以及乙商场的A,B品牌冰箱的销售利润都不变.若无论甲商场销售A品牌冰箱多少台,这100台冰箱全部售完后企业总利润保持不变,求$a$的值.
(1)请根据题意补全A,B品牌冰箱调配情况的表格(单位:台):
70-x
x-10
(2)若甲、乙两家商场全部卖出这100台冰箱的总利润为22700元,求$x$的值.
30
(3)为了促销,企业决定仅对甲商场的A品牌冰箱每台降价$a$元销售,甲商场的B品牌冰箱以及乙商场的A,B品牌冰箱的销售利润都不变.若无论甲商场销售A品牌冰箱多少台,这100台冰箱全部售完后企业总利润保持不变,求$a$的值.
10
答案:
解:
(1)$70-x$ $x-10$
(2)由题意,得$300x+200(70-x)+250(40-x)+160(x-10)=22700$,解得$x=30$.
(3)这100台冰箱全部售完后企业总利润为$(300-a)x+200(70-x)+250(40-x)+160(x-10)=(10-a)x+22400$.$\because$无论甲商场销售A品牌冰箱多少台,这100台冰箱全部售完后企业总利润保持不变,$\therefore 10-a=0$,解得$a=10$.
(1)$70-x$ $x-10$
(2)由题意,得$300x+200(70-x)+250(40-x)+160(x-10)=22700$,解得$x=30$.
(3)这100台冰箱全部售完后企业总利润为$(300-a)x+200(70-x)+250(40-x)+160(x-10)=(10-a)x+22400$.$\because$无论甲商场销售A品牌冰箱多少台,这100台冰箱全部售完后企业总利润保持不变,$\therefore 10-a=0$,解得$a=10$.
查看更多完整答案,请扫码查看


