《2025年南方新课堂金牌学案九年级数学上册人教版》

1. 如图,AB是⊙O的直径,BC,CD,DA是⊙O的弦,且BC = CD = DA,求∠BCD的度数.

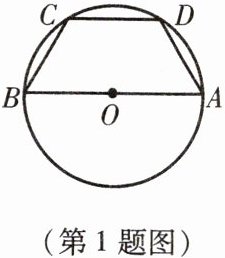
答案： $120°$.

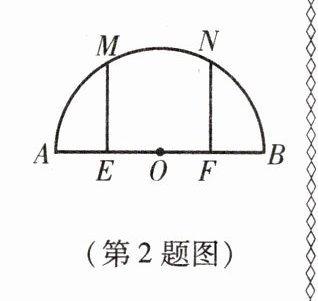
2. 如图,AB是半圆的直径,E为OA的中点,F为OB的中点,EM⊥AB于点E,NF⊥AB于点F,求证：$\overset{\frown}{AM}= \overset{\frown}{MN}= \overset{\frown}{NB}$.

答案：
如图，连接$AM$，$OM$，$ON$和$NB$. $\because ME$和$NF$分别为$OA$，$OB$的垂直平分线，$\therefore AM=OM$，$NB=ON$. 又$\because OM=ON=OA=OB$，$\therefore OA=OM=MA=OB=ON=NB$. $\therefore \angle AOM=\angle BON=60°$. $\therefore \angle MON=60°$. $\therefore \widehat{AM}=\widehat{MN}=\widehat{NB}$.

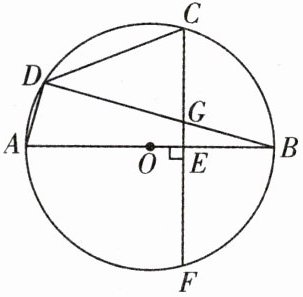
如图,AB是⊙O的直径,点C为$\overset{\frown}{BD}$的中点,CF为⊙O的弦,且CF⊥AB,垂足为E,连接BD交CF于点G,连接CD,AD,BF.
(1) 求证：△BFG≌△CDG；
(2) 若AD = BE = 2,求BF的长.

答案：
(1)证明:连接$BC$，$\because$点$C$是$\widehat{BD}$的中点，$\therefore \widehat{CD}=\widehat{BC}$. $\because AB$是$\odot O$的直径，且$CF\perp AB$，$\therefore \widehat{BC}=\widehat{BF}$. $\therefore \widehat{CD}=\widehat{BF}$. $\therefore CD=BF$. $\widehat{BD}=\widehat{CF}$. $\therefore BD=CF$. 在$\triangle BCD$和$\triangle CBF$中，$\begin{cases} CD=BF, \\ BD=CF, \\ BC=CB. \end{cases}$ $\therefore \triangle BCD\cong\triangle CBF$（SSS）. $\therefore \angle BDC=\angle F$. 在$\triangle BFG$和$\triangle CDG$中，$\begin{cases} \angle F=\angle CDG, \\ \angle FGB=\angle DGC, \\ BF=CD. \end{cases}$ $\therefore \triangle BFG\cong\triangle CDG$（AAS）.
(2)解:连接$OC$，交$BD$于点$H$，$\because C$是$\widehat{BD}$的中点，$\therefore OC\perp BD$，$DH=BH$. $\because OA=OB$，$\therefore OH=\frac{1}{2}AD=1$. $\because OC=OB$，$\angle COE=\angle BOH$，$\angle OHB=\angle OEC=90°$，$\therefore \triangle COE\cong\triangle BOH$（AAS）. $\therefore OE=OH=1$. $\therefore OC=OB=OE+BE=1+2=3$. $\therefore EF=CE=\sqrt{3^2 - 1^2}=2\sqrt{2}$. $\therefore BF=\sqrt{BE^2 + EF^2}=\sqrt{2^2 + (2\sqrt{2})^2}=2\sqrt{3}$.