第67页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
例2 试分析正方形的四个顶点是否在同一个圆上,如果在同一个圆上,请画出这个圆,并说出它的圆心和半径;如果不在同一个圆上,请说明理由.
答案:
解 正方形的四个顶点在同一个圆上,其中圆心是对角线的交点,半径为对角线长的一半. 理由如下:
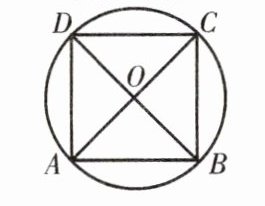
如图,$\because四边形ABCD$是正方形,$\therefore AO = BO = CO = DO$.
$\therefore A$,$B$,$C$,$D$在同一个圆上.
解 正方形的四个顶点在同一个圆上,其中圆心是对角线的交点,半径为对角线长的一半. 理由如下:

如图,$\because四边形ABCD$是正方形,$\therefore AO = BO = CO = DO$.
$\therefore A$,$B$,$C$,$D$在同一个圆上.
1. 下列图形中,哪一个图形无论绕中心旋转多少度,都能与自身重合?(
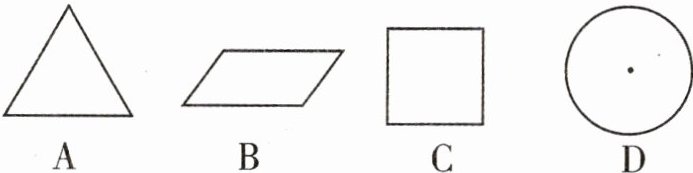
D
)
答案:
D
2. 下列四个命题中不正确的是(
A.直径是弦
B.三角形的外心到三角形三个顶点的距离都相等
C.顶点在圆周上的角是圆周角
D.半径相等的两个半圆是等弧
C
).A.直径是弦
B.三角形的外心到三角形三个顶点的距离都相等
C.顶点在圆周上的角是圆周角
D.半径相等的两个半圆是等弧
答案:
C
3. 在一个平面内到定点的距离等于定长的点都在
同一个圆上
.
答案:
同一个圆上
4. 圆的圆心和半径决定圆的
位置和大小
.
答案:
位置和大小
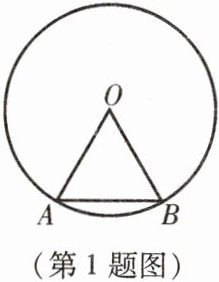
1. 如图,在半径为$a\ cm的\odot O$中,弦$AB长a\ cm$,求$\angle AOB$的度数,并计算点$O到AB$的距离.

答案:
∠AOB=60°,点 O 到 AB 的距离为$\frac{a}{2}\sqrt{3}\ cm$.
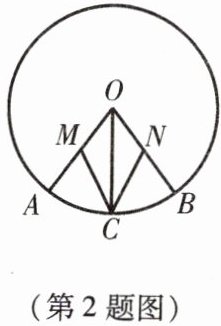
2. 如图,已知$OA$,$OB$,$OC是\odot O$的三条半径,$\angle AOC = \angle BOC$,$M$,$N分别是OA$,$OB$的中点,那么$MC与NC$相等吗?为什么?

答案:
MC=NC,理由如下:
∵OA,OB 是$\odot O$的半径,
∴OA=OB. 又
∵M,N 分别是 OA,OB 的中点,
∴OM=ON. 又
∵∠AOC=∠BOC,OC=OC,
∴△MOC≌△NOC.
∴MC=NC.
∵OA,OB 是$\odot O$的半径,
∴OA=OB. 又
∵M,N 分别是 OA,OB 的中点,
∴OM=ON. 又
∵∠AOC=∠BOC,OC=OC,
∴△MOC≌△NOC.
∴MC=NC.
查看更多完整答案,请扫码查看


