《2025年南方新课堂金牌学案九年级数学上册人教版》

3. 某工厂大门是抛物线形状,门的地面宽度是 $ 20 $ m,门的最高点离地面 $ 8 $ m,若以抛物线的顶点为原点,以抛物线的对称轴为 $ y $ 轴建立坐标系,则此抛物线的函数解析式是$y = -\dfrac{2}{25}x^{2}$.

答案： $y = -\dfrac{2}{25}x^{2}$

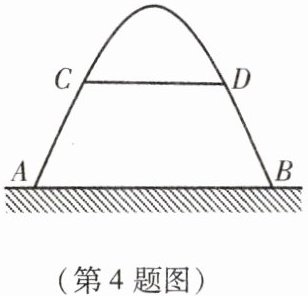
4. 如图,有一个横断面为抛物线形的水泥门洞,门洞内的地面宽 $ AB = 8 $ m. 两侧距地面 $ 4 $ m 高处各有一盏灯 $ C $,$ D $,且 $ CD = 6 $ m. 求这个门洞的高度.(精确到 $ 0.1 $ m)

答案： 以AB所在的直线为x轴，以抛物线的对称轴为y轴建立直角坐标系(如图).
∵AB = 8，
∴A(-4,0)，B(4,0). 故可设抛物线为$y = a(x - 4)(x + 4)$. 又
∵CD = 6，AB，CD相距4m，
∴C(-3,4)，D(3,4). 把点D(3,4)代入$y = a(x - 4)(x + 4)$，得$a = -\dfrac{4}{7}$.
∴$y = -\dfrac{4}{7}(x - 4)(x + 4)=-\dfrac{4}{7}x^{2}+\dfrac{64}{7}$，即抛物线$y = -\dfrac{4}{7}x^{2}+\dfrac{64}{7}$.
∴抛物线的顶点坐标是$\left(0,\dfrac{64}{7}\right)$. $\dfrac{64}{7}\approx9.1$，故这个门洞的高度约为9.1m.

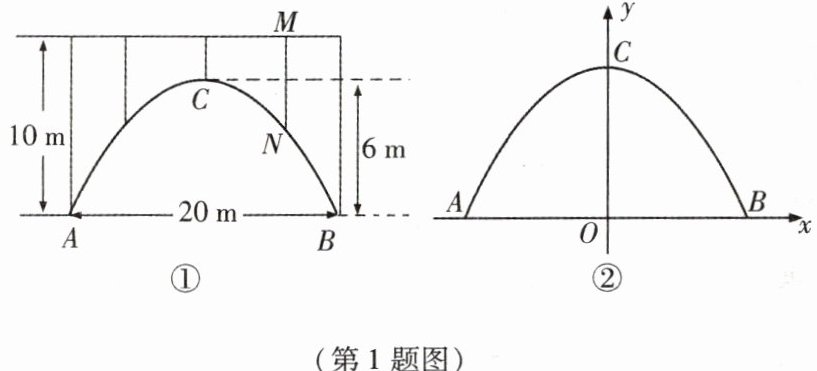
1. 一座拱桥的轮廓是抛物线(如图①所示),拱高 $ 6 $ m,跨度 $ 20 $ m,相邻两支柱间的距离均为 $ 5 $ m.
(1)将抛物线放在所给的直角坐标系中(如图②所示),其关系式为 $ y = ax^{2} + c $ 的形式,请根据所给的数据求出 $ a $,$ c $ 的值；
(2)求支柱 $ MN $ 的长度；
(3)拱桥下地平面是双向行车道(正中间是一条宽 $ 2 $ m 的隔离带),其中的一条行车道能否并排行驶宽 $ 2 $ m、高 $ 3 $ m 的三辆汽车？(汽车间的间隔忽略不计)请说明你的理由.

答案：
(1)
∵C(0,6)，B(10,0)，
∴c = 6，100a + c = 0.
∴$a = -\dfrac{3}{50}$，c = 6.
(2)$y = -\dfrac{3}{50}x^{2}+6$，把点N的横坐标x = 5代入，得y = 4.5，
∴MN = 10 - 4.5 = 5.5(m).
(3)可以. 理由如下：把y = 3代入$y = -\dfrac{3}{50}x^{2}+6$，得$x = \pm5\sqrt{2}$. 设抛物线第一象限的点P的纵坐标为3，则$P(5\sqrt{2},3)$. 作PD⊥OB于点D，则$OD = 5\sqrt{2}$，而$OD - 1\approx6.07$(m)，故可以.

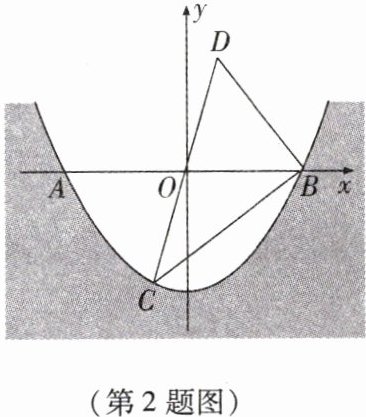
2. 某水渠的横截面呈抛物线形,水面的宽为 $ AB $(单位：m). 现以 $ AB $ 所在直线为 $ x $ 轴,以抛物线的对称轴为 $ y $ 轴建立如图所示的平面直角坐标系. 已知 $ AB = 8 $ m,设抛物线的解析式为 $ y = ax^{2} - 4 $.
(1)求 $ a $ 的值；
(2)点 $ C (-1, m) $ 是抛物线上一点,点 $ C $ 关于原点 $ O $ 的对称点为点 $ D $,连接 $ CD $,$ BC $,$ BD $. 求 $ \triangle BCD $ 的面积.

答案：
(1)
∵AB = 8，由抛物线的对称性可知OB = 4，
∴B(4,0)，0 = 16a - 4.
∴$a = \dfrac{1}{4}$.
(2)过点C作CE⊥AB于点E，过点D作DF⊥AB于点F.
∵$a = \dfrac{1}{4}$，
∴$y = \dfrac{1}{4}x^{2}-4$. 把C(-1,m)代入，得$m = \dfrac{1}{4}×(-1)^{2}-4$，
∴$m = -\dfrac{15}{4}$.
∴$C\left(-1,-\dfrac{15}{4}\right)$.
∵点C关于原点的对称点为D，
∴$D\left(1,\dfrac{15}{4}\right)$.
∴$CE = DF = \dfrac{15}{4}$.
∴$S_{\triangle BCD}=\dfrac{1}{2}OB\cdot DF+\dfrac{1}{2}OB\cdot CE=\dfrac{1}{2}×4×\dfrac{15}{4}+\dfrac{1}{2}×4×\dfrac{15}{4}=15$($m^{2}$).