第29页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1. 观察教材第 32 页二次函数 $ y = 2x^2 + 1 $,$ y = 2x^2 $,$ y = 2x^2 - 1 $ 的图象,填表:
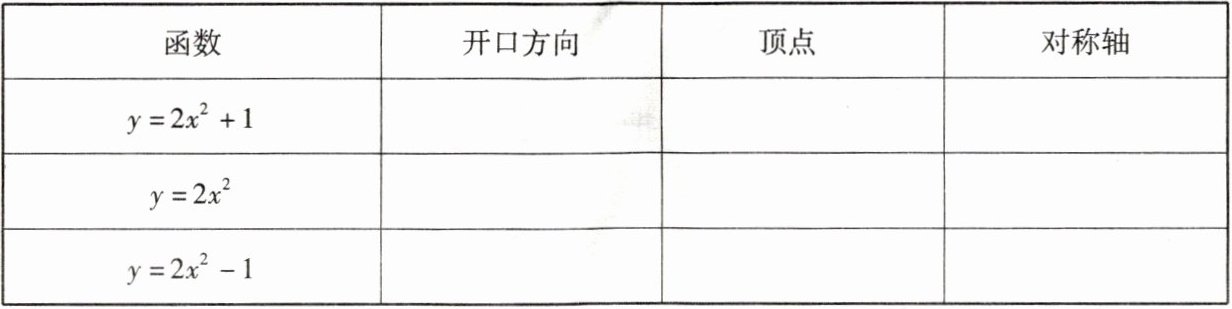

答案:
|函数|开口方向|顶点|对称轴|
| $ y = 2x^2 + 1 $ |向上|$(0,1)$|直线$x=0$|
| $ y = 2x^2 $ |向上|$(0,0)$|直线$x=0$|
| $ y = 2x^2 - 1 $ |向上|$(0,-1)$|直线$x=0$|
| $ y = 2x^2 + 1 $ |向上|$(0,1)$|直线$x=0$|
| $ y = 2x^2 $ |向上|$(0,0)$|直线$x=0$|
| $ y = 2x^2 - 1 $ |向上|$(0,-1)$|直线$x=0$|
2. 观察教材第 34 页二次函数 $ y = -\frac{1}{2}(x + 1)^2 $,$ y = -\frac{1}{2}x^2 $,$ y = -\frac{1}{2}(x - 1)^2 $ 的图象,填表:
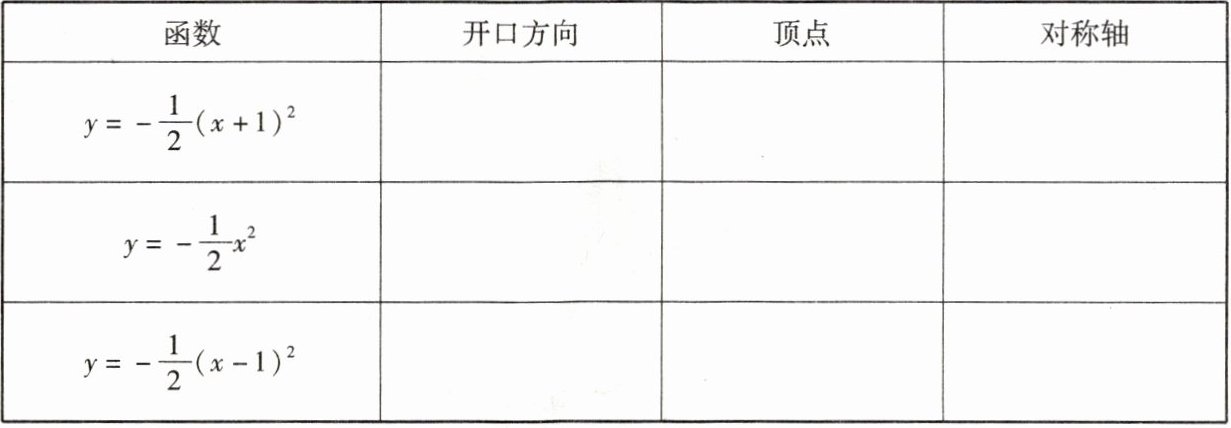

答案:
|函数|开口方向|顶点|对称轴|
| ---- | ---- | ---- | ---- |
|$y=-\frac{1}{2}(x + 1)^2$|向下|$(-1,0)$|直线$x=-1$|
|$y=-\frac{1}{2}x^2$|向下|$(0,0)$|直线$x=0$(y轴)|
|$y=-\frac{1}{2}(x - 1)^2$|向下|$(1,0)$|直线$x=1$|
| ---- | ---- | ---- | ---- |
|$y=-\frac{1}{2}(x + 1)^2$|向下|$(-1,0)$|直线$x=-1$|
|$y=-\frac{1}{2}x^2$|向下|$(0,0)$|直线$x=0$(y轴)|
|$y=-\frac{1}{2}(x - 1)^2$|向下|$(1,0)$|直线$x=1$|
例 画出二次函数 $ y = -\frac{1}{2}(x + 2)^2 $,$ y = -\frac{1}{2}(x - 2)^2 $ 的图象,并回答下列问题:
(1) 说出它们的开口方向、对称轴及顶点坐标;
(2) 抛物线 $ y = -\frac{1}{2}(x + 2)^2 $,$ y = -\frac{1}{2}(x - 2)^2 $ 与 $ y = -\frac{1}{2}x^2 $ 有什么关系?
(1) 说出它们的开口方向、对称轴及顶点坐标;
(2) 抛物线 $ y = -\frac{1}{2}(x + 2)^2 $,$ y = -\frac{1}{2}(x - 2)^2 $ 与 $ y = -\frac{1}{2}x^2 $ 有什么关系?
答案:
解 先列表:

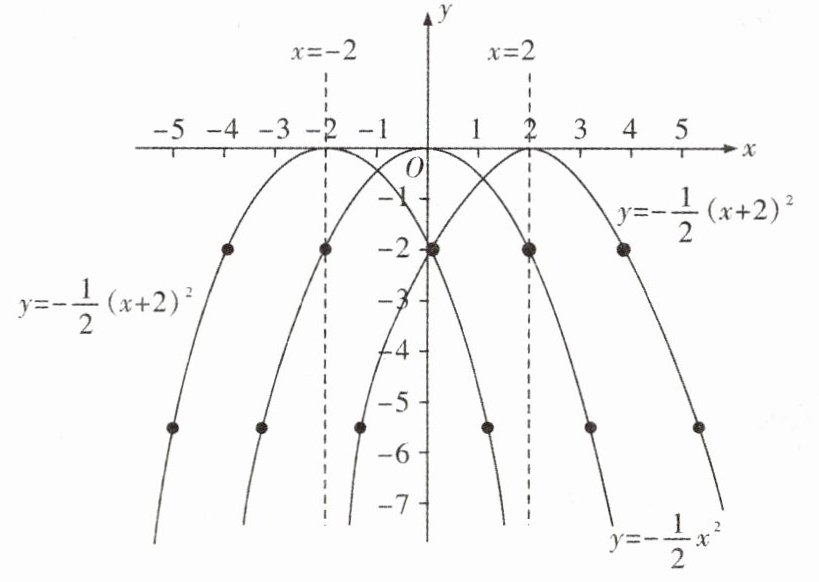
然后描点画图,得 $ y = -\frac{1}{2}(x + 2)^2 $,$ y = -\frac{1}{2}(x - 2)^2 $ 的图象(如图)。
(1) 抛物线 $ y = -\frac{1}{2}(x + 2)^2 $ 的开口向下,对称轴是 $ x = -2 $,顶点是 $ (-2, 0) $;
抛物线 $ y = -\frac{1}{2}(x - 2)^2 $ 的开口向下,对称轴是 $ x = 2 $,顶点是 $ (2, 0) $。
(2) 可以发现,把抛物线 $ y = -\frac{1}{2}x^2 $ 向左平移 2 个单位长度,就得到抛物线 $ y = -\frac{1}{2}(x + 2)^2 $;把抛物线 $ y = -\frac{1}{2}x^2 $ 向右平移 2 个单位长度,就得到抛物线 $ y = -\frac{1}{2}(x - 2)^2 $。
解 先列表:


然后描点画图,得 $ y = -\frac{1}{2}(x + 2)^2 $,$ y = -\frac{1}{2}(x - 2)^2 $ 的图象(如图)。
(1) 抛物线 $ y = -\frac{1}{2}(x + 2)^2 $ 的开口向下,对称轴是 $ x = -2 $,顶点是 $ (-2, 0) $;
抛物线 $ y = -\frac{1}{2}(x - 2)^2 $ 的开口向下,对称轴是 $ x = 2 $,顶点是 $ (2, 0) $。
(2) 可以发现,把抛物线 $ y = -\frac{1}{2}x^2 $ 向左平移 2 个单位长度,就得到抛物线 $ y = -\frac{1}{2}(x + 2)^2 $;把抛物线 $ y = -\frac{1}{2}x^2 $ 向右平移 2 个单位长度,就得到抛物线 $ y = -\frac{1}{2}(x - 2)^2 $。
查看更多完整答案,请扫码查看


