第51页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
4. [新题型]周末朵朵要去雀儿山公园玩。
(1)右图是从朵朵家到雀儿山公园的导航信息,想知道从朵朵家到雀儿山公园大约有多远,还需要知道(
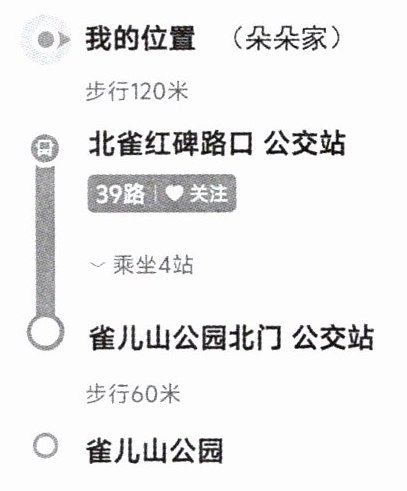
①朵朵步行用了3分钟
②朵朵乘坐公交车用了10分钟
③39路公交车每相邻两站间的距离是500米
(2)按(1)的条件,朵朵妈妈从公园骑电动车回家,每分钟行驶362米,8分钟后能到家吗?请说明理由。
(1)右图是从朵朵家到雀儿山公园的导航信息,想知道从朵朵家到雀儿山公园大约有多远,还需要知道(
③
)。(填序号)
①朵朵步行用了3分钟
②朵朵乘坐公交车用了10分钟
③39路公交车每相邻两站间的距离是500米
(2)按(1)的条件,朵朵妈妈从公园骑电动车回家,每分钟行驶362米,8分钟后能到家吗?请说明理由。
公交车行驶距离:4×500=2000(米)
总距离:120+2000+60=2180(米)
妈妈8分钟行驶距离:362×8=2896(米)
2896>2180,能到家。
总距离:120+2000+60=2180(米)
妈妈8分钟行驶距离:362×8=2896(米)
2896>2180,能到家。
答案:
(1)③
(2)公交车行驶距离:4×500=2000(米)
总距离:120+2000+60=2180(米)
妈妈8分钟行驶距离:362×8=2896(米)
2896>2180,能到家。
(1)③
(2)公交车行驶距离:4×500=2000(米)
总距离:120+2000+60=2180(米)
妈妈8分钟行驶距离:362×8=2896(米)
2896>2180,能到家。
5. [新题型]他们说得对吗?对的在$□$里画“$√$”,并举一个例子;错的在$□$里画“$×$”,并举一个反例。
|小珍|小云|小美|
|两个数相乘的积一定大于这两个数相加的和。|三位数乘一位数,乘数中间有0,积的中间也一定有0。|三位数乘一位数,乘数末尾有0,积的末尾也一定有0。|

(1)小珍$□$ 举例:
(2)小云$□$ 举例:
(3)小美$□$ 举例:
|小珍|小云|小美|
|两个数相乘的积一定大于这两个数相加的和。|三位数乘一位数,乘数中间有0,积的中间也一定有0。|三位数乘一位数,乘数末尾有0,积的末尾也一定有0。|

(1)小珍$□$ 举例:
×;$1 × 1=1$,$1+1 = 2$,$1\lt2$
(2)小云$□$ 举例:
×;$105× 3=315$,积中间没有$0$
(3)小美$□$ 举例:
√;$210× 3 = 630$,积末尾有$0$
答案:
(1)小珍$×$ 举例:$1 × 1=1$,$1+1 = 2$,$1\lt2$;
(2)小云$×$ 举例:$105× 3=315$,积中间没有$0$;
(3)小美$√$ 举例:$210× 3 = 630$,积末尾有$0$。
(2)小云$×$ 举例:$105× 3=315$,积中间没有$0$;
(3)小美$√$ 举例:$210× 3 = 630$,积末尾有$0$。
查看更多完整答案,请扫码查看


