《2025年人教金学典同步解析与测评八年级数学上册人教版重庆专版》

19. 某个圆形盘子如图①所示,其外圆半径是$R\mathrm{cm}$,内圆半径是$r\mathrm{cm}$。现在要给盘子环形部分上釉(图②阴影部分),如果$R= 10.25$,$r= 8.25$,请求出阴影部分的面积。(结果保留$\pi$)

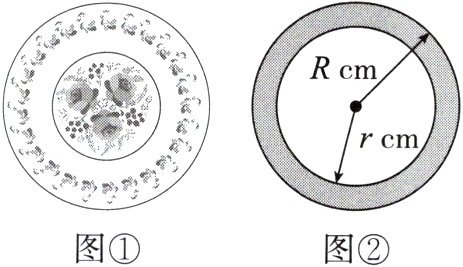
答案： 解:$\pi R^{2}-\pi r^{2}=\pi(R^{2}-r^{2})=\pi(R+r)\cdot(R-r)=\pi×(10.25+8.25)×(10.25-8.25)=37\pi$.答:阴影部分的面积为$37\pi\ cm^{2}$.

20. 已知三角形的三边长分别为$a$,$b$,$c$,且满足$a^{2}+b^{2}+c^{2}-ab-bc-ca= 0$,判断该三角形的形状。

答案： 解:将等式两边同时乘 2,得$2a^{2}+2b^{2}+2c^{2}-2ab-2bc-2ca=0$,即$(a^{2}-2ab+b^{2})+(a^{2}-2ca+c^{2})+(b^{2}-2bc+c^{2})=0$,整理,得$(a-b)^{2}+(a-c)^{2}+(b-c)^{2}=0$,所以$a-b=0$,$a-c=0$,$b-c=0$,所以$a=b=c$,所以该三角形是等边三角形.

21. 先分解因式,再求值：$(4x+5y)^{2}-(3x-2y)^{2}$,其中$x= \frac{1}{7}$,$y= 1$。

答案： 解:原式$=[(4x+5y)+(3x-2y)]\cdot[(4x+5y)-(3x-2y)]=(7x+3y)\cdot(x+7y)$.当$x=\dfrac{1}{7}$,$y=1$时,原式$=(7x+3y)(x+7y)=\dfrac{200}{7}$.