第58页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
1. 下列式子运算正确的是 (
A.$x^{3}+x^{2}= x^{5}$
B.$x^{3}\cdot x^{3}= x^{9}$
C.$(x^{3})^{4}= x^{7}$
D.$x^{9}÷ x^{3}= x^{6}$
D
)A.$x^{3}+x^{2}= x^{5}$
B.$x^{3}\cdot x^{3}= x^{9}$
C.$(x^{3})^{4}= x^{7}$
D.$x^{9}÷ x^{3}= x^{6}$
答案:
D 解析:$x^{3}$与$x^{2}$不是同类项,不能合并,故选项 A 不符合题意;$x^{3}\cdot x^{3}=x^{6}$,故选项 B不符合题意;$(x^{3})^{4}=x^{12}$,故选项 C 不符合题意;$x^{9}÷ x^{3}=x^{6}$,故选项 D 符合题意.
2. 计算$(x^{2}\cdot x^{6})^{3}$的结果是 (
A.$x^{36}$
B.$x^{20}$
C.$x^{24}$
D.$x^{15}$
C
)A.$x^{36}$
B.$x^{20}$
C.$x^{24}$
D.$x^{15}$
答案:
C 解析:$(x^{2}\cdot x^{6})^{3}=(x^{8})^{3}=x^{24}.$
3. 下列变形不正确的是 (
A.$a^{10}= (a^{2})^{5}$
B.$a^{2mn}= (a^{2})^{mn}$
C.$8^{25}= (8^{20})^{5}$
D.$(a + b)^{6}= [(a + b)^{2}]^{3}$
C
)A.$a^{10}= (a^{2})^{5}$
B.$a^{2mn}= (a^{2})^{mn}$
C.$8^{25}= (8^{20})^{5}$
D.$(a + b)^{6}= [(a + b)^{2}]^{3}$
答案:
C 解析:$8^{25}=8^{5×5}=(8^{5})^{5}.$
4. 计算$-(-\frac{2}{3}a^{2}b^{3})^{2}\cdot (-3a^{3}b^{2})^{2}$的结果为 (
A.$4a^{10}b^{10}$
B.$-2a^{10}b^{10}$
C.$2a^{10}b^{10}$
D.$-4a^{10}b^{10}$
D
)A.$4a^{10}b^{10}$
B.$-2a^{10}b^{10}$
C.$2a^{10}b^{10}$
D.$-4a^{10}b^{10}$
答案:
D 解析:$-\left(-\dfrac{2}{3}a^{2}b^{3}\right)^{2}\cdot(-3a^{3}b^{2})^{2}$$=-\dfrac{4}{9}a^{4}b^{6}\cdot9a^{6}b^{4}=-4a^{10}b^{10}.$
5. 若$a^{m}= 2,a^{n}= 4$,则$a^{m+3n}= $ (
A.8
B.24
C.64
D.128
D
)A.8
B.24
C.64
D.128
答案:
D 解析:$a^{m+3n}=a^{m}\cdot(a^{n})^{3}=2×4^{3}=128.$
6. 计算$(3x + 2y)(2x - y)$的结果是 (
A.$2x^{2}-2y^{2}$
B.$6x^{2}+7xy - 2y^{2}$
C.$6x^{2}-7xy - 2y^{2}$
D.$6x^{2}+xy - 2y^{2}$
D
)A.$2x^{2}-2y^{2}$
B.$6x^{2}+7xy - 2y^{2}$
C.$6x^{2}-7xy - 2y^{2}$
D.$6x^{2}+xy - 2y^{2}$
答案:
D 解析:$(3x+2y)(2x-y)=6x^{2}-3xy+4xy-2y^{2}=6x^{2}+xy-2y^{2}.$
7. 小明在做作业的时候,不小心把墨水滴到了作业本上,$■\cdot 3ab = 6ab - 3ab^{3}$,阴影部分即为被墨水弄污的部分,则被墨水遮住的部分是 (
A.$(2 - b^{2})$
B.$(2 + 2b)$
C.$(3ab + 2b^{2})$
D.$(2ab + b^{2})$
A
)A.$(2 - b^{2})$
B.$(2 + 2b)$
C.$(3ab + 2b^{2})$
D.$(2ab + b^{2})$
答案:
A 解析:根据题意,得■$=(6ab-3ab^{3})÷(3ab)=2-b^{2}$,因此被墨水遮住的部分为$(2-b^{2})$,故选项 A 正确.
8. 计算$(1 + 3x)(3x - 1)+9(\frac{1}{3}-x)(x+\frac{1}{3})$的结果是 (
A.$18x^{2}-2$
B.$2 - 18x^{2}$
C.0
D.$8x^{2}$
C
)A.$18x^{2}-2$
B.$2 - 18x^{2}$
C.0
D.$8x^{2}$
答案:
C 解析:原式$=(3x)^{2}-1^{2}+9\left[\left(\dfrac{1}{3}\right)^{2}-x^{2}\right]=9x^{2}-1+1-9x^{2}=0.$
9. 若计算$(3x^{2}+2ax + 1)\cdot (-3x)-4x^{2}的结果中不含x^{2}$项,则$a$的值为(
A.2
B.0
C.$-\frac{2}{3}$
D.$-\frac{3}{2}$
C
)A.2
B.0
C.$-\frac{2}{3}$
D.$-\frac{3}{2}$
答案:
C 解析:$(3x^{2}+2ax+1)\cdot(-3x)-4x^{2}$$=-9x^{3}-6ax^{2}-3x-4x^{2}$$=-9x^{3}+(-6a-4)x^{2}-3x.$因为结果中不含$x^{2}$项,所以$-6a-4=0$,解得$a=-\dfrac{2}{3}.$
10. 如图,两个正方形的边长分别为$a,b$,已知$a + b = 7,ab = 9$,则阴影部分的面积为 (
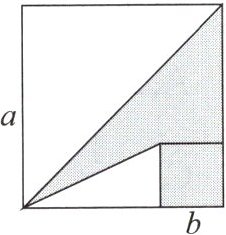
A.10
B.11
C.12
D.13
B
)
A.10
B.11
C.12
D.13
答案:
B 解析:根据题意可得,$S_{阴影}=a^{2}-\dfrac{1}{2}a^{2}-\dfrac{1}{2}(a-b)b$$=\dfrac{1}{2}(a^{2}-ab+b^{2})$$=\dfrac{1}{2}[(a+b)^{2}-3ab].$把$a+b=7,ab=9$代入上式,得$S_{阴影}=\dfrac{1}{2}×(7^{2}-3×9)=11.$
11. 计算:$(\pi - 3.14)^{0}+(-3)^{2}= $
10
.
答案:
10 解析:原式$=1+9=10.$
12. 若$2x + y - 2 = 0$,则$5^{2x}\cdot 5^{y}= $
25
.
答案:
25 解析:因为$2x+y-2=0$,所以$2x+y=2$,所以$5^{2x}\cdot5^{y}=5^{2x+y}=5^{2}=25.$
13. 若$2^{2n + 3}+4^{n + 1}= 192$,则$n$的值为 ______
2
.
答案:
2 解析:因为$2^{2n + 3}+4^{n + 1}= 192$,所以$2^{2n+3}+2^{2n+2}=192$,所以$2×2^{2n+2}+2^{2n+2}=192$,所以$3×2^{2n+2}=192$,所以$2^{2n+2}=64$,所以$2n+2=6$,所以$n=2.$
14. 已知$a = 16^{31},b = 8^{41},c = 4^{61}$,则$a,b,c$的大小关系是
$c\lt b\lt a$
.(用“$<$”连接)
答案:
$c\lt b\lt a$ 解析:$a=16^{31}=(2^{4})^{31}=2^{124}$;$b=8^{41}=(2^{3})^{41}=2^{123}$;$c=4^{61}=(2^{2})^{61}=2^{122}.$因为$124>123>122$,所以$2^{124}>2^{123}>2^{122}$,即$c\lt b\lt a$.
查看更多完整答案,请扫码查看


