《2025年人教金学典同步解析与测评八年级数学上册人教版重庆专版》

1. 已知在$\triangle ABC$中,$\angle A= \angle B-\angle C$,则$\triangle ABC$为(C)
A.锐角三角形
B.钝角三角形
C.直角三角形
D.以上都有可能

答案： C　解析:因为在△ABC中,∠A+∠B+∠C=180°,且∠A=∠B-∠C,所以2∠B=180°,所以∠B=90°,故△ABC是直角三角形.故选C.

2. 如图,在$\triangle ABC$中,$CD是边AB$上的高,$\angle BCD= 30^{\circ}$,$\angle ACB= 80^{\circ}$,$AE是\angle CAB$的平分线,则$\angle AEB$的度数是______.

100°

答案： 100°　解析:因为CD是△ABC的边AB上的高,所以∠CDB=∠CDA=90°.因为∠BCD=30°,∠ACB=80°,所以∠ACD=∠ACB−∠BCD=50°,∠CBD=90°−∠BCD=60°,所以∠CAB=90°−∠ACD=40°.因为AE是∠CAB的平分线，所以∠EAB=$\frac{1}{2}$∠CAB=20°,所以∠AEB=180°−∠EAB−∠EBA=100°.

3. 如图,$C处在B处的北偏西40^{\circ}$方向,$C处在A处的北偏西75^{\circ}$方向,则$\angle ACB$的度数为______.

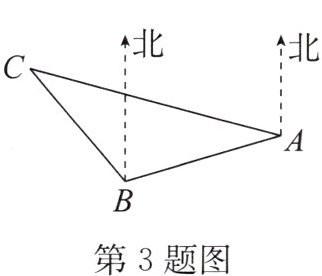
答案：
35°　解析:如图,∠DBA+∠BAE=180°.因为∠CAE=75°,所以∠DBA+∠BAC=105°.因为∠CBD=40°,所以∠CBA+∠BAC=145°,所以∠ACB=180°−145°=35°.
　　　　　　

4. (新定义题)在一个三角形中,如果一个内角是另一个内角的$3$倍,那么这样的三角形我们称为“三倍角三角形”.例如,一个三角形的三个内角分别为$120^{\circ}$,$40^{\circ}$,$20^{\circ}$,则这个三角形是“三倍角三角形”.
(1)在$\triangle ABC$中,$\angle A= 35^{\circ}$,$\angle B= 40^{\circ}$,$\triangle ABC$是“三倍角三角形”吗？为什么？
(2)若$\triangle ABC$是“三倍角三角形”,且$\angle B= 30^{\circ}$,求$\triangle ABC$中最小内角的度数.

答案： 解:
(1)△ABC是“三倍角三角形”.理由如下:因为∠A=35°,∠B=40°,所以∠C=180°−35°−40°=105°=3∠A,所以△ABC是“三倍角三角形”.
(2)由题意可知,∠A+∠C=150°.设最小内角的度数为x.①若30°=3x,则x=10°,180°−30°-10°=140°,成立.②若x+3x=150°,则x=37.5°,30°＜37.5°,所以不成立.③若x=30°,则30°×3=90°,180°−30°−90°=60°,成立.所以△ABC中最小内角的度数为10°或30°.

5. 在$\triangle ABC$中,$AD$是角平分线,$\angle B＜\angle C$,
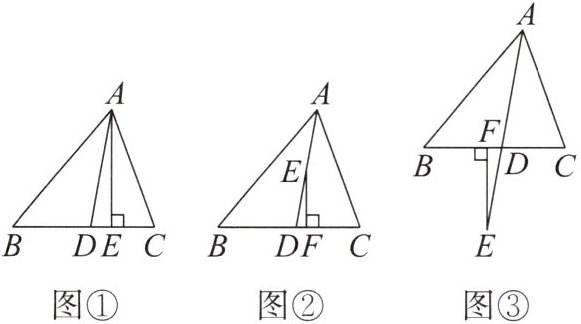
(1)如图①,$AE是\triangle ABC$的高,$\angle B= 50^{\circ}$,$\angle C= 70^{\circ}$,求$\angle DAE$的度数.
(2)如图②,点$E在AD$上,$EF\perp BC于点F$,试探究$\angle DEF与\angle B$,$\angle C$的数量关系,并证明你的结论.
(3)如图③,点$E在AD$的延长线上,$EF\perp BC于点F$,此时(2)中的结论还成立吗？试说明理由.

答案：
解:
(1)因为AD是∠BAC的平分线，所以∠CAD=$\frac{1}{2}$∠BAC.因为AE⊥BC,所以∠CAE=90°−∠C,所以∠DAE=∠CAD−∠CAE =$\frac{1}{2}$∠BAC−(90°−∠C)=$\frac{1}{2}$(180°−∠B−∠C)−(90°−∠C)=$\frac{1}{2}$∠C−$\frac{1}{2}$∠B=$\frac{1}{2}$(∠C−∠B).因为∠B=50°,∠C=70°,所以∠DAE=$\frac{1}{2}$×(70°−50°)=10°.
(2)∠DEF=$\frac{1}{2}$(∠C−∠B).证明如下:如图,过点A作AG⊥BC于点G.
　　　　　　　
因为EF⊥BC,所以AG//EF，所以∠DAG=∠DEF.由
(1)可得,∠DAG=$\frac{1}{2}$(∠C−∠B),所以∠DEF=$\frac{1}{2}$(∠C−∠B).
(3)成立.理由如下:如图,过点A作AG⊥BC于点G.
　　　　　　　
因为EF⊥BC,所以AG//EF，所以∠DAG=∠DEF.由
(1)可得,∠DAG=$\frac{1}{2}$(∠C−∠B),所以∠DEF=$\frac{1}{2}$(∠C−∠B),所以
(2)中的结论成立.