《2025年人教金学典同步解析与测评八年级数学上册人教版重庆专版》

9. 如图,在 $ \triangle ABC $ 中,$ AB = AC $,$ D $ 是 $ BC $ 上的一点,在 $ AB $,$ AC $ 上分别截取 $ BE = CD $,$ CF = BD $,连接 $ DE $,$ DF $,$ EF $,$ AD $。有下列结论：① $ \angle EDF = 90° - \frac{1}{2}\angle BAC $；② $ \angle EDF = \angle B $；③ $ AD \perp BC $；④ $ \angle DEF = \angle DFE $。其中正确结论的序号是(①②④)

A.①②
B.②④
C.①②③
D.①②④

答案： D　解析:在△ABC中,AB = AC,所以∠B = ∠C = $\frac{1}{2}$(180° - ∠BAC)=90° - $\frac{1}{2}$∠BAC.在△BDE和△CFD中,$\begin{cases} BE = CD, \\ ∠B = ∠C, \\ BD = CF, \end{cases}$所以△BDE≌△CFD(SAS),所以DE = DF,∠BED = ∠CDF.因为∠BDE + ∠EDF + ∠CDF = 180°,所以∠EDF = 180° - (∠BDE + ∠CDF)=180° - (∠BDE + ∠BED).因为∠BDE + ∠BED = 180° - ∠B,所以∠EDF = 180° - (180° - ∠B)=∠B = 90° - $\frac{1}{2}$∠BAC,故①②正确.因为DE = DF,所以∠DEF = ∠DFE,故④正确.因为AB = AC，所以当AD⊥BC时,AD平分∠BAC,AD是BC的中线，所以∠BAD = ∠CAD,BD = CD.根据题意，可得D是BC上的一点，所以当点D是BC的中点时,AD⊥BC,否则AD,BC不一定垂直,故③错误.综上所述，正确的有①②④.　故选D.

10. 如图,在 $ \triangle ABC $ 中,$ \angle ABC = 60° $,$ AD $ 平分 $ \angle BAC $ 交 $ BC $ 于点 $ D $,$ CE $ 平分 $ \angle ACB $ 交 $ AB $ 于点 $ E $,$ AD $,$ CE $ 交于点 $ F $。有下列说法：① $ \angle AFC = 120° $；② $ S_{\triangle ABD} = S_{\triangle ADC} $；③若 $ AB = 2AE $,则 $ CE \perp AB $；④ $ CD + AE = AC $；⑤ $ S_{\triangle AEF}:S_{\triangle FDC} = AF:FC $。其中说法正确的序号是( )

A.①②③
B.①③④
C.②③⑤
D.①③④⑤

答案：
D　解析:因为∠ABC = 60°,所以∠BAC + ∠ACB = 180° - ∠ABC = 120°.因为AD平分∠BAC,CE平分∠ACB，所以∠DAC = $\frac{1}{2}$∠BAC,∠ECA = $\frac{1}{2}$∠ACB,所以∠DAC + ∠ECA = $\frac{1}{2}$(∠BAC + ∠ACB)=60°,所以∠AFC = 180° - (∠DAC + ∠ECA)=120°,故①正确.如图①,过点D作DG⊥AB于点G,DG⊥AC于点H,则DG = DH.因为AB与AC不一定相等,所以$\frac{1}{2}AB\cdot DG$与$\frac{1}{2}AC\cdot DH$不一定相等.即S△ABD与S△ADC不一定相等,故②错误.　　　　 如图①,延长CE到点K,使KE = CE,连接BK.因为AB = 2AE,所以BE = AE.在△BKE和△ACE中,$\begin{cases} KE = CE, \\ ∠BEK = ∠AEC, \\ BE = AE, \end{cases}$所以△BKE≌△ACE(SAS),所以∠K = ∠ACE,BK = AC.因为∠BCE = ∠ACE,所以∠BCE = ∠K,所以BK = BC,所以AC = BC,所以CE⊥AB,故③正确.如图②,在AC上截取AL = AE,连接FL.因为∠AFC = 120°,所以∠AFE = ∠CFD = 180° - ∠AFC = 60°.在△ALF和△AEF中,$\begin{cases} AL = AE, \\ ∠LAF = ∠EAF, \\ AF = AF, \end{cases}$所以△ALF≌△AEF(SAS),所以∠AFL = ∠AFE = 60°,所以∠CFL = ∠AFC - ∠AFL = 60°,所以∠CFL = ∠CFD.在△FLC和△FDC中,$\begin{cases} ∠LCF = ∠DCF, \\ CF = CF, \\ ∠CFL = ∠CFD, \end{cases}$所以△FLC≌△FDC(ASA),所以CL = CD,所以CD + AE = CL + AL = AC,故④正确.　　　　　 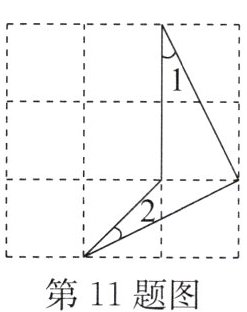如图②,过点L作LM⊥FA于点M,LN⊥FC于点N.因为∠AFL = ∠CFL,所以LM = LN,所以$\frac{S_{\triangle ALF}}{S_{\triangle FLC}}=\frac{\frac{1}{2}AF\cdot LM}{\frac{1}{2}FC\cdot LN}=\frac{AF}{FC}$.因为S△ALF = S△AEF,S△FLC = S△FDC,所以S△AEF:S△FDC = AF:FC,故⑤正确.所以说法正确的是①③④⑤.故选D.

11. 如图,已知方格纸中有 9 个相同的小正方形,则 $ \angle 1 + \angle 2 $ 的度数为 $ $ $° $。

答案：
45　解析:如图,观察图形可知∠3与∠1所在的直角三角形全等(两直角边长分别为1和2),所以∠1 = ∠3.　因为∠4 = 45°,　所以∠1 + ∠2 = ∠3 + ∠2 = ∠4 = 45°.　　　　　　　

12. 如图,$ \triangle ABC $ 和 $ \triangle A'B'C' $ 关于直线 $ l $ 对称,若 $ \angle A = 50° $,$ \angle C' = 30° $,则 $ \angle B $ 的度数为 100°。

答案： 100°　解析:由题意,知∠C = ∠C' = 30°,所以∠B = 180° - 50° - 30° = 100°.

13. 如图,$ \triangle ABC \cong \triangle DEC $,点 $ B $,$ C $,$ D $ 在同一直线上,若 $ CE = 4 $,$ AC = 7 $,则 $ BD $ 的长为 $ 11$。

答案： 11　解析:因为△ABC≌△DEC,所以BC = CE = 4,CD = AC = 7.因为点B,C,D在同一直线上,所以BD = BC + CD = 11.

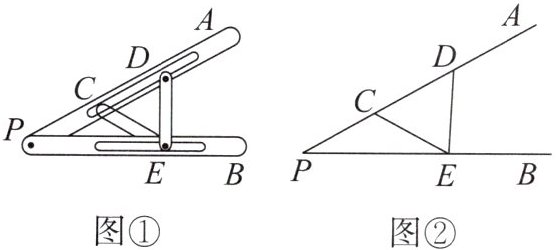
14. “三等分角”是古希腊三大几何问题之一,借助如图①所示的三等分角仪可以三等分角。这个三等分角仪的示意图如图②所示,有公共端点 $ P $ 的两条线段 $ PA $,$ PB $,可以绕点 $ P $ 转动,点 $ C $ 固定,点 $ D $,$ E $ 在槽中可以滑动,且 $ CE = DE = CP $。若 $ \angle DEB = 87° $,则 $ \angle P $ 的度数为 $ $29$° $。

答案： 29　解析:因为CE = DE = CP,所以∠P = ∠CEP,∠ECD = ∠EDC.因为∠ECD = ∠P + ∠CEP = 2∠P,所以∠EDC = 2∠P.　因为∠P + ∠CDE = ∠DEB,　所以3∠P = ∠DEB.　因为∠DEB = 87°,所以∠P = 29°.