第44页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
1.(跨学科融合)下面是物理教材中部分电路元件的符号,其中不是轴对称图形的是(
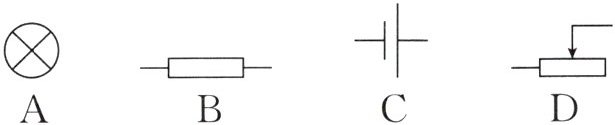
D
)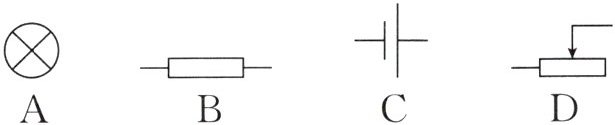
答案:
D
2. 在平面直角坐标系中,点 $ A(-2,m - 1) $ 与点 $ B(n + 2,3) $ 关于 $ x $ 轴对称,则 $ m + n $ 的值是(
A.-6
B.4
C.5
D.-5
A
)A.-6
B.4
C.5
D.-5
答案:
A 解析:由题意可得−2=n+2,m - 1 = −3,解得n = −4,m = −2,所以m + n = −6. 故选A.
3. 一个三角形两边的长分别是 3 和 5,则这个三角形第三边的长可能是(
A.1
B.1.5
C.2
D.4
D
)A.1
B.1.5
C.2
D.4
答案:
D 解析:设三角形第三边的长为x,则5 - 3<x<5 + 3,即2<x<8,只有选项D符合题意. 故选D.
4. 画 $ \triangle ABC $ 的边 $ AB $ 上的高,下列画法中,正确的是(
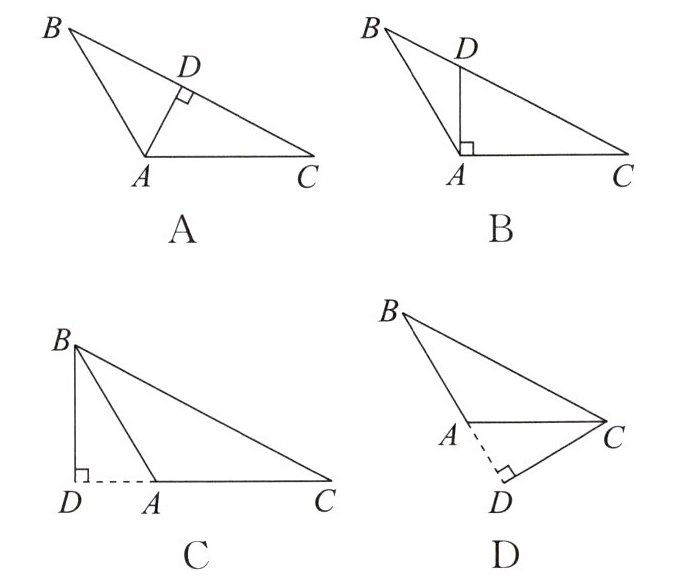
D
)
答案:
D 解析:根据三角形高的定义可知,边AB上的高是从点C向AB作垂线,顶点C与垂足之间的线段. 故选D.
5. 如图,在 $ Rt\triangle ABC $ 中,$ CD $ 是斜边 $ AB $ 上的高,$ \angle B = 30° $,$ AD = 2\ cm $,则 $ AB $ 的长度是(
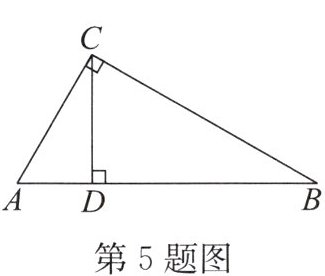
A.8 cm
B.6 cm
C.4 cm
D.2 cm
A
)
A.8 cm
B.6 cm
C.4 cm
D.2 cm
答案:
A 解析:在Rt△ABC中,CD是斜边AB上的高,所以∠B + ∠A = ∠DCA + ∠A = 90°, 所以∠DCA = ∠B = 30°, 所以AC = 2AD = 4cm, 所以AB = 2AC = 8cm. 故选A.
6. 雨伞在开合过程中某时刻的截面示意图如图所示,伞骨 $ AB = AC $,点 $ D $,$ E $ 分别是 $ AB $,$ AC $ 的中点,$ DM $,$ EM $ 是连接弹簧和伞骨的支架,且 $ DM = EM $,已知弹簧 $ M $ 在向上滑动的过程中,总有 $ \triangle ADM \cong \triangle AEM $,其判定依据是(
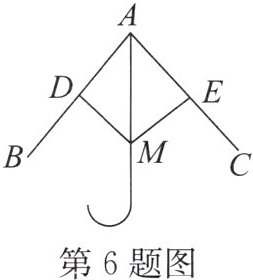
A.ASA
B.AAS
C.SSS
D.HL
C
)
A.ASA
B.AAS
C.SSS
D.HL
答案:
C 解析:因为AB = AC,点D,E分别是AB,AC的中点,所以AD = AE. 又因为DM = EM,AM是公共边, 所以判定依据是“SSS”.
7. 如图,把 $ \triangle ABC $ 经过一定的变换得到 $ \triangle A'B'C' $,若 $ \triangle ABC $ 上一点 $ P $ 的坐标为 $ (x,y) $,这个点经过同样的变换后得到点 $ P' $,则点 $ P' $ 的坐标为(
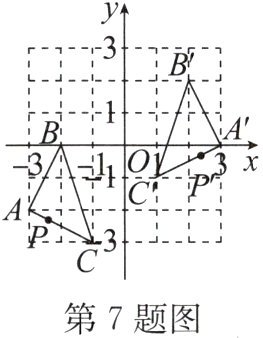
A.$ (-x,y - 2) $
B.$ (-x + 2,-y) $
C.$ (-x,y + 2) $
D.$ (-x + 2,y + 2) $
C
)
A.$ (-x,y - 2) $
B.$ (-x + 2,-y) $
C.$ (-x,y + 2) $
D.$ (-x + 2,y + 2) $
答案:
C 解析:因为把△ABC向上平移2个单位长度,再关于y轴对称可得到△A'B'C',所以点P'的坐标为( - x,y + 2). 故选C.
8. 如图,在 $ \triangle ABC $ 中,$ \angle C = 90° $,$ BC = 6 $,$ AC = 8 $,$ AB = 10 $,以点 $ B $ 为圆心,适当长为半径作弧,分别交 $ AB $,$ BC $ 于点 $ M $,$ N $,再分别以点 $ M $ 和点 $ N $ 为圆心,大于 $ \frac{1}{2}MN $ 的长为半径作弧(弧所在圆的半径都相等),两弧交于点 $ E $,作射线 $ BE $ 交 $ AC $ 于点 $ D $,则线段 $ CD $ 的长为( )
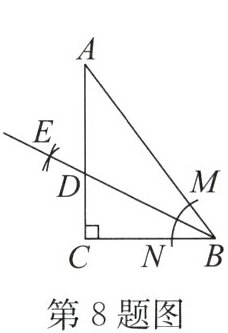
A.2
B.3
C.5
D.6

A.2
B.3
C.5
D.6
答案:
B 解析:如图,过点D作DF⊥AB于点F,设CD = x. 由作图,知BE平分∠ABC. 因为∠C = 90°,DF⊥AB, 所以DF = CD = x. 因为S△ABC = S△ADB + S△BDC, 所以$\frac{1}{2}AC\cdot BC=\frac{1}{2}AB\cdot DF+\frac{1}{2}CD\cdot BC$.因为BC = 6,AC = 8,AB = 10, 所以$\frac{1}{2}×8×6=\frac{1}{2}×10x+\frac{1}{2}×6x$, 解得x = 3,即CD = 3. 故选B.
由作图,知BE平分∠ABC. 因为∠C = 90°,DF⊥AB, 所以DF = CD = x. 因为S△ABC = S△ADB + S△BDC, 所以$\frac{1}{2}AC\cdot BC=\frac{1}{2}AB\cdot DF+\frac{1}{2}CD\cdot BC$.因为BC = 6,AC = 8,AB = 10, 所以$\frac{1}{2}×8×6=\frac{1}{2}×10x+\frac{1}{2}×6x$, 解得x = 3,即CD = 3. 故选B.
B 解析:如图,过点D作DF⊥AB于点F,设CD = x.
 由作图,知BE平分∠ABC. 因为∠C = 90°,DF⊥AB, 所以DF = CD = x. 因为S△ABC = S△ADB + S△BDC, 所以$\frac{1}{2}AC\cdot BC=\frac{1}{2}AB\cdot DF+\frac{1}{2}CD\cdot BC$.因为BC = 6,AC = 8,AB = 10, 所以$\frac{1}{2}×8×6=\frac{1}{2}×10x+\frac{1}{2}×6x$, 解得x = 3,即CD = 3. 故选B.
由作图,知BE平分∠ABC. 因为∠C = 90°,DF⊥AB, 所以DF = CD = x. 因为S△ABC = S△ADB + S△BDC, 所以$\frac{1}{2}AC\cdot BC=\frac{1}{2}AB\cdot DF+\frac{1}{2}CD\cdot BC$.因为BC = 6,AC = 8,AB = 10, 所以$\frac{1}{2}×8×6=\frac{1}{2}×10x+\frac{1}{2}×6x$, 解得x = 3,即CD = 3. 故选B. 查看更多完整答案,请扫码查看


