《2025年人教金学典同步解析与测评八年级数学上册人教版重庆专版》

9. 如图,在$\triangle ABC$中,$AB = AC$,$AD$,$CE是\triangle ABC$的两条中线,$P是AD$上的一个动点,则下列线段的长度等于$BP + EP$最小值的是( )

A.$BC$
B.$CE$
C.$AD$
D.$AC$

答案：
B 解析:如图,连接PC.

因为AB=AC,BD=CD,所以AD⊥BC,所以PB=PC,所以PB+PE=PC+PE.因为PE+PC≥CE,所以当P,C,E共线时,PB+PE的值最小,最小值为CE的长度.故选B.

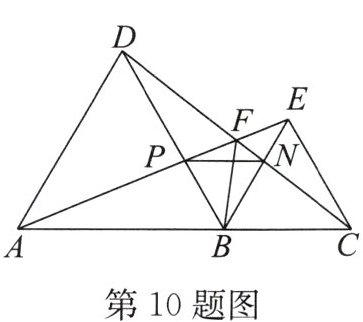
10. 如图,点$A$,$B$,$C$在一条直线上,$\triangle ABD$,$\triangle BCE$均为等边三角形,连接$AE$,$CD$,$AE交BD于点P$,$CD交BE于点N$,$AE与CD交于点F$,连接$PN$,$BF$.下列结论：①$\triangle ABE \cong \triangle DBC$；②$\angle DFA = 60^{\circ}$；③$\triangle BPN$为等边三角形；④$FB平分\angle AFC$.其中正确的结论有(A)

A.4 个
B.3 个
C.2 个
D.1 个

答案： A 解析:因为△ABD,△BCE为等边三角形,所以AB=DB,∠ABD=∠CBE=60°,BE=BC,所以∠ABE=∠DBC,∠PBN=60°.在△ABE和△DBC中,$\begin{cases} AB=DB, \\ ∠ABE=∠DBC, \\ BE=BC, \end{cases}$所以△ABE≌△DBC(SAS),所以①正确.因为△ABE≌△DBC,所以∠BAE=∠BDC.因为∠BDC+∠BCD=∠ABD=60°,所以∠DFA=∠BAE+∠BCD=∠BDC+∠BCD=60°,所以②正确.在△ABP和△DBN中,$\begin{cases} ∠BAP=∠BDN, \\ AB=DB, \\ ∠ABP=∠DBN=60°, \end{cases}$所以△ABP≌△DBN(ASA),所以BP=BN,所以△BPN为等边三角形,所以③正确.因为△ABE≌△DBC,所以AE=CD,$S_{\triangle ABE}=S_{\triangle DBC}$,所以点B到AE,CD的距离相等,所以点B在∠AFC的平分线上,即FB平分∠AFC,所以④正确.所以正确的结论有4个.故选A.

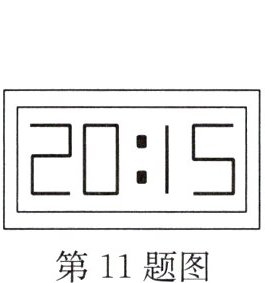
11. 小强站在镜子前,从镜中看到镜子对面墙上挂着的电子表的示数如图所示,则电子表的实际时间是21:05.

答案： 21:05 解析:以镜面的左边沿或右边沿所在的直线为对称轴,沿此直线折叠都会得到21:05,或将题中图案从反面观察,也可得到21:05.

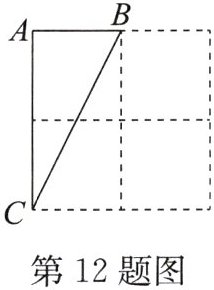
12. 如图,在$2×2$的方格纸中,有一个以格点为顶点的$\triangle ABC$,请你找出方格纸中所有与$\triangle ABC$成轴对称且也以格点为顶点的三角形,这样的三角形共有______个.

答案：
5 解析:如图,与△ABC成轴对称且也以格点为顶点的三角形有△ABD,△ACD,△FBE,△HCE,△AFG,共5个.

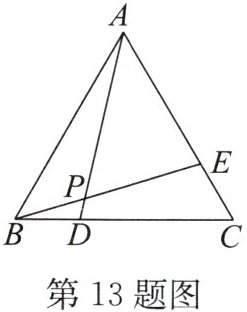
13. 如图,已知在等边三角形$ABC$中,$BD = CE$,$AD与BE相交于点P$,则$\angle APE$的度数是60°.

答案： 60° 解析:因为△ABC是等边三角形,所以∠ABD=∠C=60°,AB=BC.在△ABD和△BCE中,AB=BC,∠ABD=∠C,BD=CE,所以△ABD≌△BCE(SAS),所以∠BAD=∠CBE.因为∠ABE+∠CBE=60°,所以∠ABE+∠BAD=60°,所以∠APE=∠ABE+∠BAD=60°.

14. 如图,在$Rt\triangle ABC$中,$D$,$E为斜边AB$上的两个点,且$BD = BC$,$AE = AC$,则$\angle DCE$的度数为______.

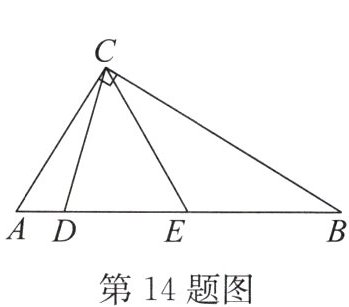
45°

答案： 45° 解析:设∠DCE=x,∠ACD=y,则∠ACE=x+y.因为∠ACB=90°,所以∠BCE=90° - ∠ACE=90° - x - y.因为AE=AC,所以∠ACE=∠AEC=x+y.因为BD=BC,所以∠BDC=∠BCD=∠BCE+∠DCE=90° - x - y + x=90° - y.因为∠DCE+∠CDE+∠DEC=180°,所以x+(90° - y)+(x + y)=180°,解得x=45°,所以∠DCE=45°.

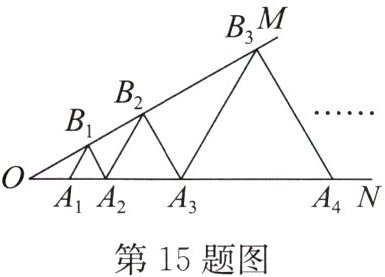
15. 如图,已知$\angle MON = 30^{\circ}$,点$A_1$,$A_2$,$A_3$,…$在射线ON$上,点$B_1$,$B_2$,$B_3$,…$在射线OM$上,$\triangle A_1B_1A_2$,$\triangle A_2B_2A_3$,$\triangle A_3B_3A_4$,…$$均为等边三角形,若$OA_1 = 1$,则$A_2A_3$的长度为2,$\triangle A_9B_9A_{10}$的边长为256.

答案： 2 256 解析:因为△A₁B₁A₂是等边三角形,所以∠B₁A₁A₂=60°,A₁A₂=A₁B₁.因为∠MON=30°,所以∠OB₁A₁=∠B₁A₁A₂ - ∠MON=30°.所以∠MON=∠OB₁A₁,所以A₁B₁=OA₁,所以A₁A₂=OA₁=1.同理可得A₂A₃=OA₂=2OA₁=2,A₃A₄=OA₃=2OA₂=2×2=2²,A₄A₅=OA₄=2OA₃=2×2²=2³,……AₙAₙ₊₁=2ⁿ⁻¹.所以△A₉B₉A₁₀的边长A₉A₁₀=2⁹⁻¹=2⁸=256.

16. 如图,在$\triangle ABC$中,$\angle ABC和\angle ACB的平分线相交于点G$,过点$G作EF // BC交AB于点E$,交$AC于点F$,过点$G作GD \perp AC于点D$,则$\angle BGC与\angle A$之间的数量关系可表示为______,设$GD = m$,$AE + AF = n$,则$S_{\triangle AEF} = $______(用$m$,$n$表示).

答案：
∠BGC=90°+$\frac{1}{2}$∠A $\frac{1}{2}$mn 解析:因为∠ABC和∠ACB的平分线相交于点G,所以∠GBC+∠GCB=$\frac{1}{2}$(∠ABC+∠ACB)=$\frac{1}{2}$(180° - ∠A),所以∠BGC=180° - (∠GBC+∠GCB)=180° - $\frac{1}{2}$(180° - ∠A)=90°+$\frac{1}{2}$∠A.连接AG,如图,因为∠ABC和∠ACB的平分线相交于点G,所以点G到△ABC各边的距离相等.因为GD=m,AE+AF=n,所以$S_{\triangle AEF}=\frac{1}{2}AE·GD+\frac{1}{2}AF·GD=\frac{1}{2}(AE+AF)·GD=\frac{1}{2}mn$.