第34页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
5. 如图,在由边长为1个单位长度的小正方形组成的网格中,$\triangle ABC$的顶点均在格点上.画出与$\triangle ABC关于直线l对称的\triangle A_1B_1C_1$($A与A_1$,$B与B_1$,$C与C_1$是对称点).连接$BB_1$,$CC_1$,并计算梯形$BB_1C_1C$的面积.
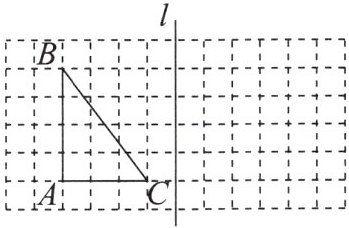

答案:
解:如图所示.由图知$CC_{1}=2,BB_{1}=8,$梯形$BB_{1}C_{1}C$的高是 4,所以$S_{梯形BB_{1}C_{1}C}=\frac {1}{2}(CC_{1}+BB_{1})×4=20.$
解:如图所示.由图知$CC_{1}=2,BB_{1}=8,$梯形$BB_{1}C_{1}C$的高是 4,所以$S_{梯形BB_{1}C_{1}C}=\frac {1}{2}(CC_{1}+BB_{1})×4=20.$

6. 如图,在平面直角坐标系中,$l$是第一、第三象限的角平分线.
(1)实验与探究:
由图观察,易知$A(0,2)关于直线l的对称点A'的坐标为(2,0)$,请在图中分别标出$B(5,3)$,$C(-2,5)关于直线l的对称点B'$,$C'$的位置,并写出它们的坐标.
(2)归纳与发现:
结合图形观察以上三组点的坐标,可以发现:坐标平面内任一点$P(m,n)$关于第一、第三象限的角平分线$l的对称点P'$的坐标为______.
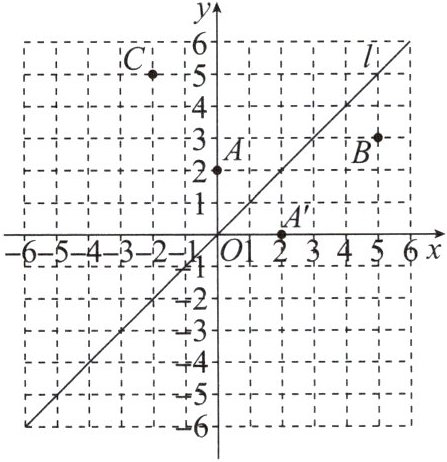
(1)实验与探究:
由图观察,易知$A(0,2)关于直线l的对称点A'的坐标为(2,0)$,请在图中分别标出$B(5,3)$,$C(-2,5)关于直线l的对称点B'$,$C'$的位置,并写出它们的坐标.
(2)归纳与发现:
结合图形观察以上三组点的坐标,可以发现:坐标平面内任一点$P(m,n)$关于第一、第三象限的角平分线$l的对称点P'$的坐标为______.

答案:
解:
(1)如图,B'(3,5),C'(5,-2).
(2)点P'的坐标为(n,m).故答案为(n,m).
解:
(1)如图,B'(3,5),C'(5,-2).

(2)点P'的坐标为(n,m).故答案为(n,m).
查看更多完整答案,请扫码查看


