《2025年人教金学典同步解析与测评八年级数学上册人教版重庆专版》

1. 在三角形中,到三个顶点距离相等的点是(D)
A.三条高所在直线的交点
B.三条中线的交点
C.三条角平分线的交点
D.三边垂直平分线的交点

答案： 1.D　解析:因为线段垂直平分线上的点与这条线段两个端点的距离相等，所以在三角形中，到三个顶点距离相等的点是三边垂直平分线的交点.

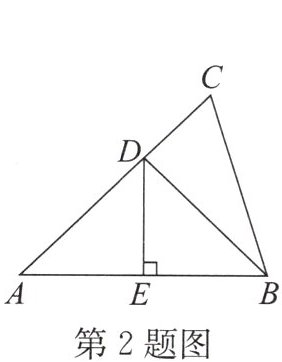
2. 如图,在△ABC中,边AB的垂直平分线分别交AC,AB于点D,E,若AE= 3,△BCD的周长为8,则△ABC的周长为(C)

A.8
B.11
C.14
D.18

答案： 2.C　解析:因为DE是线段AB的垂直平分线,所以AB=2AE=6,DA=DB.因为△BCD的周长为8,所以BD+CD+BC=8，所以AD+CD+BC=8,所以AC+BC=8.因为AB=6,所以△ABC的周长为AB+BC+AC=6+8=14.故选C.

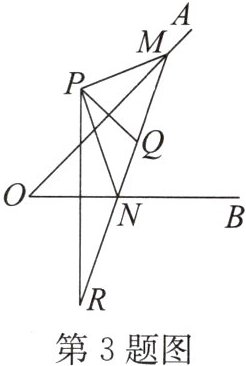
3. 如图,点P是∠AOB外的一点,点M,N分别是∠AOB两边上的点,点P关于OA的对称点Q恰好落在线段MN上,点P关于OB的对称点R落在MN的延长线上.若PM= 2.5 cm,PN= 3 cm,MN= 4 cm,则线段QR的长为(4.5cm)

A.4.5 cm
B.5.5 cm
C.6.5 cm
D.7 cm

答案： 3.A　解析:由题意，知OA垂直平分PQ,所以MQ=PM=2.5cm,同理,NR=PN=3cm,所以QN=MN−QM=4−2.5=1.5(cm),QR=QN+NR=1.5+3=4.5(cm).

4. “如果m,n互为倒数,那么mn= 1”的逆命题是真命题.

答案： 4.真　解析:命题“如果m,n互为倒数,那么mn=1”的逆命题是“如果mn=1,那么m，n互为倒数”,逆命题是真命题.

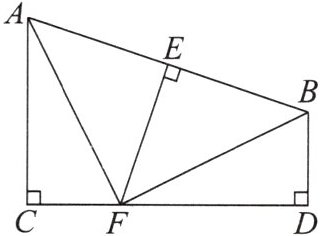
5. 如图,AC⊥CD,BD⊥CD,AB的垂直平分线EF交AB于点E,交CD于点F,且AC= FD,则△ABF的形状是等腰直角三角形.

答案： 5.等腰直角三角形　解析:因为EF是AB的垂直平分线,所以AF=BF.在Rt△ACF和Rt△FDB中,$\left\{\begin{array}{l} AF=FB,\\ AC=FD,\end{array}\right. $所以Rt△ACF≌Rt△FDB(HL).所以∠AFC=∠FBD.因为∠FBD+∠BFD=90°,所以∠AFC+∠BFD=90°,所以∠AFB=90°,所以△ABF是等腰直角三角形.

6. 如图所示,A,B,C三点表示三个村庄,为了让村民子女就近入学,计划新建一所小学,要使三个村庄到学校的距离相等,请你在图中确定学校的位置.

答案：
6.解:
(1)连接AB,BC;
(2)分别作AB,BC的垂直平分线,两条垂直平分线交于点P,则点P就是所要确定的学校的位置(如图所示).

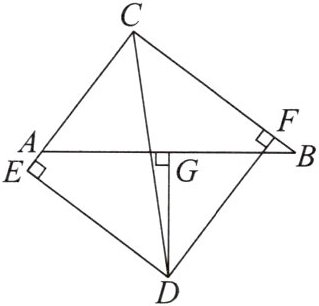
7. 如图,在△ABC中,∠BCA的平分线CD与AB边的垂直平分线DG相交于点D,DE⊥AC交CA的延长线于点E,DF⊥BC于点F.求证：AE= BF.

答案：
7.证明:如图,连接AD,BD. 因为CD平分∠BCA,DE⊥AC,DF⊥BC,所以DE=DF.因为DG是AB的垂直平分线,所以DA=DB.在Rt△ADE和Rt△BDF中,$\left\{\begin{array}{l} DA=DB,\\ DE=DF,\end{array}\right. $所以Rt△ADE≌Rt△BDF(HL).所以AE=BF.