《2025年人教金学典同步解析与测评八年级数学上册人教版重庆专版》

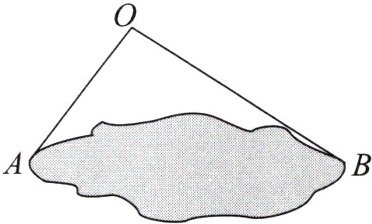
1. 如图,小明为了估计池塘两岸 $ A $,$ B $ 间的距离,在池塘一侧选取了点 $ O $,测得 $ OA = 6 \, m $,$ OB = 9 \, m $,那么 $ A $,$ B $ 间的距离不可能是(D)

A.$ 6 \, m $
B.$ 7 \, m $
C.$ 13 \, m $
D.$ 15 \, m $

答案： D 解析:在△OAB 中,OA=6 m,OB=9 m,则 OB - OA ＜ AB ＜ OB + OA,即3 m ＜ AB ＜ 15 m,所以 A,B 间的距离不可能是15 m.故选 D.

2. 一个等腰三角形的三边长分别为 $ 3 \, cm $,$ a \, cm $,$ 6 \, cm $,则它的周长是(B)
A.$ 12 \, cm $
B.$ 15 \, cm $
C.$ 12 \, cm $ 或 $ 15 \, cm $
D.不能确定

答案： B 解析:当a=3时,三角形的三边长为3 cm,3 cm,6 cm,因为3 + 3 = 6,所以不能组成三角形.当a=6时,三角形的三边长为3 cm,6 cm,6 cm,因为3 + 6 ＞ 6,所以可以组成三角形,所以周长为3 + 6 + 6 = 15(cm).故选 B.

3. 若三角形的三边长分别是 $ 3 $,$ 4 $,$ 2x - 1 $,则 $ x $ 的取值范围是(B)
A.$ 0 ＜ x ＜ 4 $
B.$ 1 ＜ x ＜ 4 $
C.$ 0 ＜ x ＜ 3 $
D.$ 1 ＜ x ＜ 3 $

答案： B 解析:根据题意,得{2x - 1 ＞ 4 - 3,3 + 4 ＞ 2x - 1},解得1 ＜ x ＜ 4.故选 B.

4. 小明说：“虽然我的新圆规的带有针尖的脚只有 $ 9 \, cm $,但我能画出半径为 $ 20 \, cm $ 的圆。”我觉得小明说的话不合理(填“合理”或“不合理”),理由是三角形两边之和大于第三边。

答案： 不合理 三角形两边之和大于第三边
解析:因为三角形两边之和大于第三边,所以带有针尖的脚只有9 cm 的圆规只能画出半径小于18 cm 的圆,故小明说的话不合理.

5. 三角形的周长小于 $ 13 $,且各边长为互不相等的整数,则这样的三角形共有3个。

答案： 3 解析:根据三角形的两边之和大于第三边以及三角形的周长小于13,知其中的任何一边不能超过6.5.根据三角形各边长为整数,所以任何一边的长都大于1,且小于6,故三边可能的长度为2,3,4,5.根据各边长都不相等可得,三边的长度为2,3,4;2,4,5;3,4,5.故这样的三角形共有3个.

6. 在学习了三角形后,老师给同学们每人准备了一根 $ 12 \, cm $ 长的木棒,让同学们通过剪拼的方式,组成一个三角形木框。
(1)小明想把木棒剪成三段,第一段长 $ a \, cm $,第二段的长比第一段的 $ 3 $ 倍少 $ 2 \, cm $。试判断第一段的长能否为 $ 3 \, cm $,并说明理由。
(2)如图,小亮先把木棒剪成 $ AB $ 和 $ CD $ 两段,已知 $ AB = 4 \, cm $,$ CD = 8 \, cm $,现要将木棒 $ CD $ 从点 $ P $ 处剪开,使得三根木棒首尾顺次相接能组成三角形,请直接写出符合条件的 $ CP $ 的整数长度。
]

答案：
(1)第一段的长不能为3 cm.理由如下:根据题意,若第一段长3 cm,则第二段的长为3×3 - 2 = 7(cm),第三段的长为12 - 3 - 7 = 2(cm).因为3 + 2 ＜ 7,所以这三根木棒不能组成一个三角形木框,所以第一段的长不能为3 cm.
(2)设 CP = x cm,则 PD = (8 - x)cm.因为 AB,CP,PD 能组成三角形,所以x + 4 ＞ 8 - x,且4 + 8 - x ＞ x,解得2 ＜ x ＜ 6,所以整数x 为3或4或5,即符合条件的CP 的整数长度为3 cm 或4 cm 或5 cm.

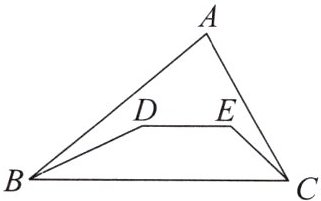
7. 如图,已知 $ D $,$ E $ 为 $ \triangle ABC $ 内两点,试说明：$ AB + AC ＞ DE + BD + CE $。

答案： 方法一:如图①,延长 DE 交 AC 于点N,延长 ED 交AB 于点M.在△AMN 中,AM + AN ＞ MD + DE + EN.①在△BMD 中,BM + DM ＞ BD.②在△CEN 中,CN + EN ＞ CE.③由①+②+③,得 AM + AN + BM + DM + CN + EN ＞ MD + DE + EN + BD + CE,所以 AM + AN + BM + CN ＞ DE + BD + CE,即 AB + AC ＞ DE + BD + CE.
方法二:如图②,延长 CE 交 AB 于点G,延长 BD 交 CG 于点 F.在△ACG 中,AG + AC ＞ GF + EF + CE.①在△BGF 中,BG + GF ＞ BD + DF.②在△DEF 中,DF + EF ＞ DE.③由①+②+③,得 AG + AC + BG + GF + DF + EF ＞ GF + EF + CE + BD + DF + DE,所以 AG + AC + BG ＞ CE + BD + DE,即 AB + AC ＞ DE + BD + CE.