《2025年人教金学典同步解析与测评八年级数学上册人教版重庆专版》

24. 学习了全等三角形的判定后, 某数学兴趣小组同学就“测量河两岸 $ A $, $ B $ 两点间的距离”这一问题, 设计了如下方案, 如图.
【测量工具】测量角度的仪器, 皮尺等.
【测量步骤】
① 在点 $ B $ 所在河岸同侧的平地上取点 $ C $ 和点 $ D $, 使得点 $ A $, $ B $, $ C $ 在同一条直线上, 且 $ CD = BC $;
② 测得 $ \angle DCB = 100° $, $ \angle ADC = 65° $;
③ 在 $ CD $ 的延长线上取点 $ E $, 使得 $ \angle BEC = 15° $;
④ 测得 $ DE $ 的长度为 30 m.
【问题解决】请你根据以上方案求出 $ A $, $ B $ 两点间的距离 $ AB $.
【延伸探究】设 $ AD $ 与 $ BE $ 交于点 $ F $, 善于观察和思考的小明同学猜想线段 $ AF = EF $, 你同意小明的观点吗? 说明理由.

答案： 24.解:【问题解决】
在△ACD中,因为∠C = 100°,∠ADC = 65°,
所以∠CAD = 15°,
所以∠CAD = ∠BEC.
在△ACD和△ECB中,
$\left\{\begin{array}{l}∠A = ∠E,\\ ∠ACD = ∠ECB,\\ CD = CB,\end{array}\right.$
所以△ACD≌△ECB(AAS).
所以AC = EC.
又因为CD = CB,所以AB = DE = 30m.
【延伸探究】
同意小明的观点.
理由:由上,知∠CAD = ∠BEC,AB = ED.
因为∠AFB与∠EFD是对顶角,
所以∠AFB = ∠EFD.
在△ABF和△EDF中,
$\left\{\begin{array}{l}∠BAF = ∠DEF,\\ ∠AFB = ∠EFD,\\ AB = ED,\end{array}\right.$
所以△ABF≌△EDF(AAS).
所以AF = EF.

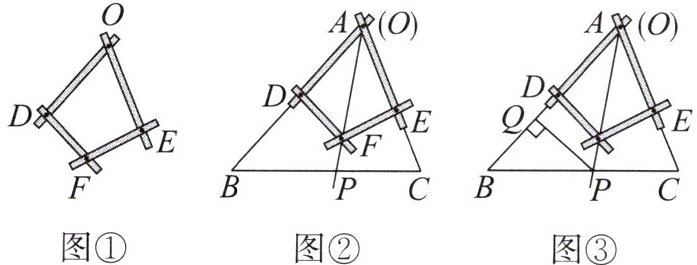
25. 图 ① 是一个平分角的仪器, 其中 $ OD = OE $, $ FD = FE $.
(1) 如图 ②, 将仪器放置在 $ \triangle ABC $ 上, 使点 $ O $ 与顶点 $ A $ 重合, $ D $, $ E $ 分别在边 $ AB $, $ AC $ 上, 沿 $ AF $ 画一条射线 $ AP $, 交 $ BC $ 于点 $ P $. $ AP $ 是 $ \angle BAC $ 的平分线吗? 请判断并说明理由.
(2) 如图 ③, 在 (1) 的条件下, 过点 $ P $ 作 $ PQ \perp AB $ 于点 $ Q $, 若 $ PQ = 4 $, $ AC = 8 $, $ \triangle ABC $ 的面积是 36, 求 $ AB $ 的长.

答案： 25.解:
(1)AP是∠BAC的平分线.理由如下:
在△ADF和△AEF中,
$\left\{\begin{array}{l}AD = AE,\\ FD = FE,\\ AF = AF,\end{array}\right.$
所以△ADF≌△AEF(SSS).
所以∠DAF = ∠EAF,
所以AP是∠BAC的平分线.
(2)过点P作PG⊥AC于点G(图略).
因为AP平分∠BAC,PQ⊥AB,
所以PG = PQ = 4.
因为S△ABC = S△ABP + S△APC = $\frac{1}{2}$AB·PQ + $\frac{1}{2}$AC·PG,
所以$\frac{1}{2}$AB×4 + $\frac{1}{2}$×8×4 = 36.
所以AB = 10.