《2025年人教金学典同步解析与测评八年级数学上册人教版重庆专版》

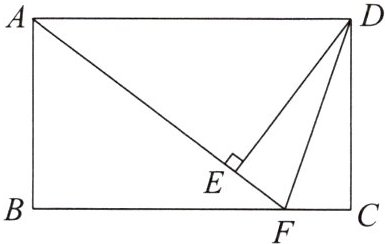
20. 如图, 已知在长方形 $ ABCD $ 中, $ F $ 是 $ BC $ 上一点, 且 $ AF = BC $, $ DE \perp AF $ 于点 $ E $, 连接 $ DF $.
求证: (1) $ \triangle ABF \cong \triangle DEA $;
(2) $ DF $ 是 $ \angle EDC $ 的平分线.

答案： 20.证明:
(1)因为AF = BC,BC = AD,
所以AF = AD.
因为DE⊥AF,∠B = 90°,
所以∠B = ∠AED.
因为AD//CB,所以∠AFB = ∠DAE.
在△ABF和△DEA中,
$\left\{\begin{array}{l}∠B = ∠AED,\\ ∠AFB = ∠DAE,\\ AF = DA,\end{array}\right.$
所以△ABF≌△DEA(AAS).
(2)由
(1),得AE = BF,所以AF - AE = BC - BF,即FE = FC.
因为DE⊥AF,DC⊥CF,
所以DF是∠EDC的平分线.

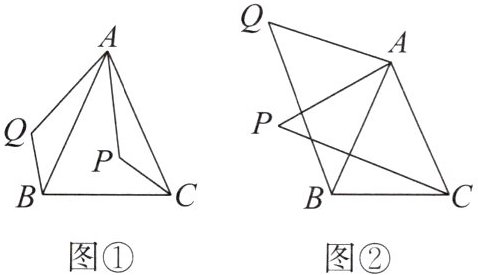
21. 在复习“全等三角形”的知识时, 老师布置了一道作业题: 如图 ①, 已知在 $ \triangle ABC $ 中, $ AB = AC $, $ P $ 是 $ \triangle ABC $ 内部任意一点, 将 $ AP $ 绕点 $ A $ 顺时针旋转至 $ AQ $, 使 $ \angle QAP = \angle BAC $, 连接 $ BQ $, $ CP $, 则 $ BQ = CP $.
小亮是个爱动脑筋的同学, 他通过对图 ① 的分析, 证明了 $ \triangle ABQ \cong \triangle ACP $, 从而证得 $ BQ = CP $ 之后, 将点 $ P $ 移到 $ \triangle ABC $ 之外, 原题中的条件不变, 发现“$ BQ = CP $”仍然成立, 请你就图 ② 给出证明.

答案： 21.解:因为∠QAP = ∠BAC,
所以∠QAP + ∠BAP = ∠BAC + ∠BAP,
即∠QAB = ∠PAC.
在△QAB和△PAC中,
$\left\{\begin{array}{l}AQ = AP,\\ ∠QAB = ∠PAC,\\ AB = AC,\end{array}\right.$
所以△QAB≌△PAC(SAS).
所以BQ = CP.