《2025年人教金学典同步解析与测评八年级数学上册人教版重庆专版》

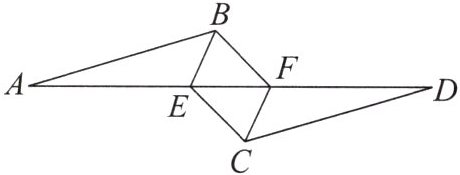
8. 如图, 已知 $ AB // CD $, $ AB = CD $, $ AE = FD $, 则图中的全等三角形有 (C)

A.1 对
B.2 对
C.3 对
D.4 对

答案： C 解析:△ABE≌△DCF,△ABF≌△DCE,△BEF≌△CFE,共3对.

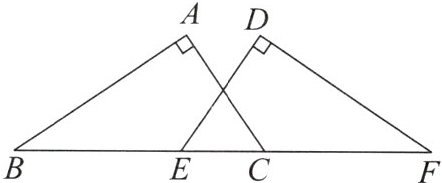
9. 如图, 在 $ \triangle ABC $ 和 $ \triangle DEF $ 中, $ \angle A = \angle D = 90° $, $ AC = DE $, 若要用“斜边、直角边 (HL)”直接证明 $ Rt \triangle ABC \cong Rt \triangle DFE $, 则还需补充条件 (D)

A.$ AB = DF $
B.$ \angle B = \angle F $
C.$ \angle ACB = \angle DEF $
D.$ BE = FC $

答案： D 解析:补充BE = FC,可得BC = EF.
在Rt△ABC和Rt△DFE中,
$\left\{\begin{array}{l}BC = FE,\\ AC = DE,\end{array}\right.$
所以Rt△ABC≌Rt△DFE(HL).
故选D.

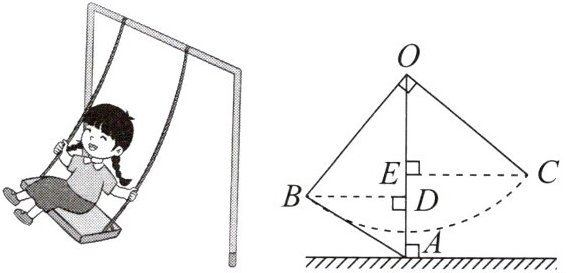
10. 小丽与爸妈在公园里荡秋千. 如图 (示意图), 小丽坐在秋千的起始位置 $ A $ 处, $ OA $ 与地面垂直, 两脚在地面上用力一蹬, 妈妈在距地面 1 m 高的 $ B $ 处接住她后用力一推, 爸爸在 $ C $ 处接住她. 若妈妈与爸爸到 $ OA $ 的水平距离 $ BD $, $ CE $ 分别为 1.4 m 和 1.8 m, $ \angle BOC = 90° $. 爸爸在 $ C $ 处接住小丽时, 小丽距离地面的高度是 (D)

A.1 m
B.1.6 m
C.1.8 m
D.1.4 m

答案： D 解析:因为∠BOC = 90°,
所以∠BOD + ∠COE = 90°.
由题意可知,OB = CO,DA = 1m,BD⊥OA,CE⊥OA,
所以∠BDO = ∠OEC = 90°,
所以∠BOD + ∠OBD = 90°,
所以∠COE = ∠OBD.
在△OBD和△COE中,
$\left\{\begin{array}{l}∠BDO = ∠OEC,\\ ∠OBD = ∠COE,\\ OB = CO,\end{array}\right.$
所以△OBD≌△COE(AAS).
所以OE = BD = 1.4m,OD = CE = 1.8m,
所以AE = OA - OE = OD + DA - OE = 1.8 + 1 - 1.4 = 1.4(m),
即小丽距离地面的高度是1.4m.
故选D.

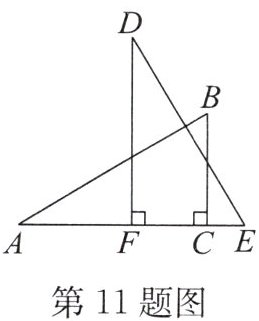
11. 如图, $ BC \perp AE $ 于点 $ C $, $ DF \perp AE $ 于点 $ F $, $ \triangle ABC \cong \triangle DEF $. 若 $ DF = 5 $, $ BC = 3 $, $ CF = 2 $, 则 $ AE $ 的长为 ______6.

答案： 11.6 解析:因为△ABC≌△DEF,DF = 5,BC = 3,CF = 2,
所以AC = DF = 5,EF = BC = 3.
所以AE = AC + EF - CF = 5 + 3 - 2 = 6.

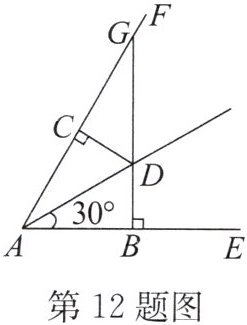
12. 如图, 若 $ DB \perp AE $ 于点 $ B $, $ DC \perp AF $ 于点 $ C $, 且 $ DC = DB $, $ \angle BAD = 30° $, 则 $ \angle DGF = $ ______150°.

答案： 12.150° 解析:因为DB⊥AE,DC⊥AF,且DC = DB,
所以AD是∠CAB的平分线,即∠CAD = ∠BAD = 30°,
所以∠GAB = 60°.
又因为∠ABG = 90°,所以∠AGB = 30°,
所以∠DGF = 150°.

13. 如图, $ \angle C = \angle D = 90° $, 有下列条件:
① $ \angle 1 = \angle 2 $, ② $ \angle 3 = \angle 4 $, ③ $ AC = BD $, ④ $ AD = BC $. 补充其中一个条件后, 不能直接判定 $ \triangle ABC \cong \triangle BAD $ 的是 ② (填序号).

答案： 13.② 解析:补充条件①可用"AAS"判定全等;补充条件③可用"HL"判定全等;补充条件④可用"HL"判定全等.
∠3与∠4不是待证的两个三角形中的角,不能直接判定两个三角形全等.

14. 如图, 已知在 $ \triangle ABC $ 中, $ AB = AC $, $ AD $ 是 $ \triangle ABC $ 的角平分线, $ DE \perp AB $ 于点 $ E $, $ DF \perp AC $ 于点 $ F $, 则下列结论:
① $ AD $ 上任意一点到点 $ C $, $ B $ 的距离相等; ② $ AD $ 上任意一点到 $ AB $, $ AC $ 的距离相等; ③ $ BD = CD $, $ AD = BC $; ④ $ \angle BDE = \angle CDF $. 正确的个数是 ______.

答案：
14.3 解析:如图,P为AD上任意一点,连接PB,PC.

在△APB与△APC中,AP = AP,AB = AC,∠BAD = ∠CAD,
所以△APB≌△APC(SAS).所以PB = PC,①正确;根据角的平分线的性质不难得出AD上任意一点到AB,AC的距离相等,②正确;不难得到△ADB≌△ADC(SAS),所以BD = CD,但无法判断AD与BC之间的关系,③错误;由△ADB≌△ADC(SAS),知∠ABC = ∠ACB,而∠BDE + ∠ABC = 90°,∠CDF + ∠ACB = 90°,所以∠BDE = ∠CDF,④正确.
故正确的个数是3.