《2025年人教金学典同步解析与测评八年级数学上册人教版重庆专版》

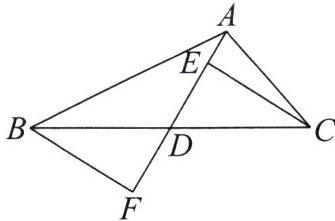
9. 如图,在$\triangle ABC$中,$AD$是中线,点$E$,$F在直线AD$上,且$CE// BF$。求证：$CE= BF$。

答案： 证明:因为AD是△ABC的中线,所以CD=BD.因为CE//BF,所以∠DCE=∠DBF,∠DEC=∠F.所以△DCE≌△DBF(AAS).所以CE=BF.

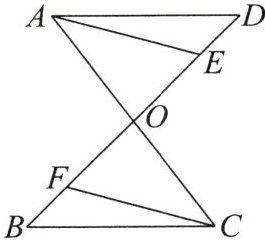
10. 如图,$AC与BD交于点O$,$AD= CB$,$E$,$F是BD$上两点,且$AE= CF$,$DE= BF$。求证：(1)$\angle D= \angle B$；(2)$AE// CF$。

答案： 证明:
(1)在△ADE和△CBF中，$\left\{\begin{array}{l} AD=CB,\\ AE=CF,\\ DE=BF,\end{array}\right. $所以△ADE≌△CBF(SSS).所以∠D=∠B.
(2)因为△ADE≌△CBF,所以∠AED=∠CFB,所以∠AEF=∠CFE,所以AE//CF.

11. 如图①,点$A$,$C$,$F$,$D$在同一条直线上,$AF= DC$,$AB= DE$,$BC= EF$。


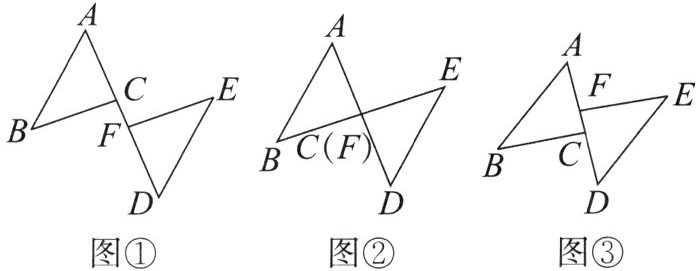
(1)试说明$AB// ED$,$BC// EF$。
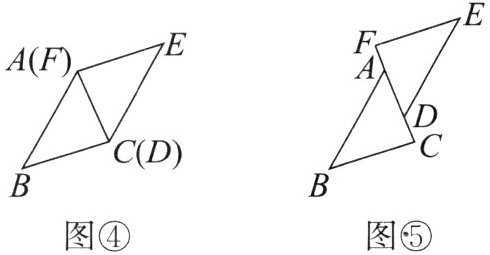
(2)把图①中的$\triangle DEF沿直线AD$平移到四个不同位置,如图②③④⑤,仍有上面的结论吗？

答案： 解:
(1)因为AF=DC,所以AF−CF=DC−CF,即AC=DF.在△ABC和△DEF中，$\left\{\begin{array}{l} AC=DF,\\ AB=DE,\\ BC=EF,\end{array}\right. $所以△ABC≌△DEF(SSS).所以∠A=∠D,∠ACB=∠DFE,所以AB//ED,∠BCF=∠EFC,所以BC//EF.
(2)在题图②中,AB//ED,BC和EF在同一条直线上;题图③④⑤中,AB//ED，BC//EF.证明方法与
(1)类似.

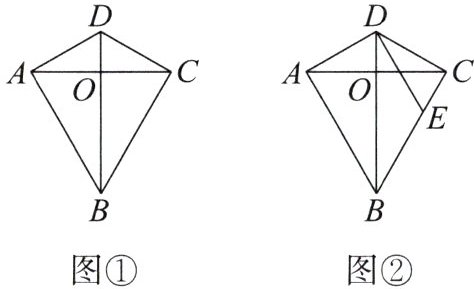
12. (新定义题)如图①,在四边形$ABCD$中,$AD= CD$,$AB= CB$。我们把这种两组邻边分别相等的四边形叫作“筝形”。
(1)试猜想筝形的对角线$AC与BD$有什么位置关系？并用全等三角形的知识证明你的猜想。
(2)如图②,过点$D作DE// AB交BC于点E$,若$BC= 10$,$CE= 3$,求$DE$的长。

答案： 解:
(1)筝形的对角线AC与BD的位置关系是BD⊥AC.证明如下:在△ABD和△CBD中，$\left\{\begin{array}{l} AD=CD,\\ AB=CB,\\ BD=BD,\end{array}\right. $所以△ABD≌△CBD(SSS).所以∠ADB=∠CDB.在△AOD和△COD中，$\left\{\begin{array}{l} AD=CD,\\ ∠ADB=∠CDB,\\ OD=OD,\end{array}\right. $所以△AOD≌△COD(SAS).所以∠AOD=∠COD.因为∠AOD+∠COD=180°,所以∠AOD=∠COD=90°,所以BD⊥AC.
(2)因为DE//AB,所以∠EDB=∠ABD.因为△ABD≌△CBD,所以∠ABD=∠CBD,所以∠EDB=∠CBD,过点E作EF⊥BD于点F(图略).由作图可知∠EFB=∠EFD=90°.在△EFB和△EFD中，$\left\{\begin{array}{l} ∠EFB=∠EFD,\\ ∠EDB=∠CBD,\\ EF=EF,\end{array}\right. $所以△EFB≌△EFD(AAS),所以DE=BE.因为BC=10,CE=3,所以BE=BC−CE=10−3=7,所以DE=BE=7.