《2025年人教金学典同步解析与测评八年级数学上册人教版重庆专版》

21. 如图,有 A,B,C 三个小岛,B 岛在 A 岛的北偏东 85°方向,A 岛在 C 岛的西南方向,B 岛在 C 岛的南偏西 20°方向,求∠ABC 的度数.

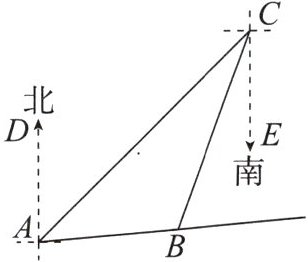
答案： 解:依题意,得∠DAB=85°,∠ACE=45°,∠BCE=20°,所以∠ACB=∠ACE-∠BCE=25°.因为AD//CE,所以∠DAC=∠ACE=45°,所以∠CAB=∠DAB-∠DAC=40°,所以∠ABC=180°-∠CAB-∠ACB=115°.

22. 如图,有一根长度为 18 cm 的木条,从两端各截取长度为 x cm 的木条.

(1)若得到的三根木条能组成等边三角形,求 x 的值；
(2)若得到的三根木条能组成三角形,写出 x 的取值范围.

答案： 解:
(1)根据题意可知,三根木条的长度分别为x cm,x cm,(18-2x)cm,所以x=18-2x,解得x=6,即x的值为6.
(2)根据题意可知,三根木条的长度分别为x cm,x cm,(18-2x)cm.当x-(18-2x)≥0,即x≥6时,则x+(18-2x)＞x,解得x＜9.所以6≤x＜9.当x-(18-2x)＜0,即x＜6时,则x+x＞18-2x,解得x＞ $\frac{9}{2}$.所以 $\frac{9}{2}$＜x＜6.综上所述,x的取值范围是 $\frac{9}{2}$＜x＜9.

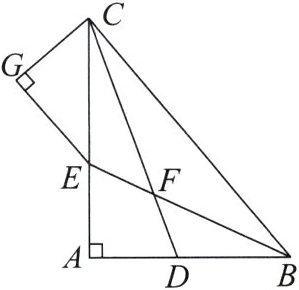
23. 如图,在 Rt△ABC 中,∠A = 90°,CD,BE 是角平分线,它们相交于点 F,EG // BC,CG ⊥ EG,垂足为 G.
(1)求∠BFD 的度数；
(2)求证：∠ADC = ∠GCD.

答案：
(1)解:在Rt△ABC中,∠A=90°,所以∠ABC+∠ACB=90°.因为BE平分∠ABC,CD平分∠ACB,所以∠FBC= $\frac{1}{2}$∠ABC,∠BCF= $\frac{1}{2}$∠ACB,所以∠FBC+∠FCB= $\frac{1}{2}$(∠ABC+∠ACB)= $\frac{1}{2}$×90°=45°,所以∠BFD=∠FBC+∠FCB=45°.
(2)证明:因为EG//BC,CG⊥EG,所以CG⊥BC,所以∠BCG=90°.因为CD平分∠ACB,所以∠ACD=∠BCD.因为∠ADC+∠ACD=∠GCD+∠BCD=90°,所以∠ADC=∠GCD.