第49页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
13. 新考法 新定义
2024·南通海门区月考
如图甲所示,小明和小华在探究光的折射现象时,将一束入射角为 $ 50^{\circ} $ 的光斜射入杯中的水里,更换杯中的介质时他们发现光的偏折程度不同。为了定量反映这种差异,小明将“折射角与入射角的比值”定义为“偏折比”,并根据所学物理知识和生活经验,对影响“偏折比”大小的因素提出以下猜想:
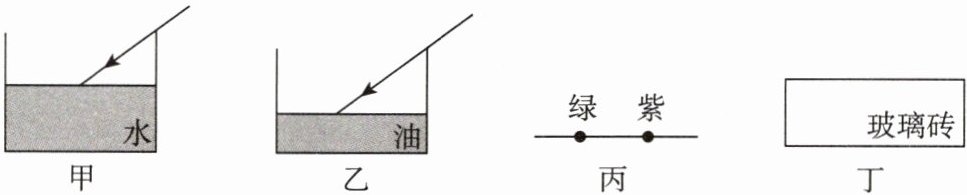
猜想 1:“偏折比”与液面的高度有关。
猜想 2:“偏折比”与液体的种类有关。
猜想 3:“偏折比”与入射光的颜色有关。
(1) 小华认为猜想 1 是错误的,其理由是
(2) 为了验证猜想 2,小明只将图甲中的水换成油。如图乙所示,油的高度小于水的高度,杯底光斑的位置恰与图甲实验时光斑的位置重合,对比可知:在相同条件下,油对光的“偏折比”
(3) 为了探究猜想 3,小明用图甲装置先后射入绿色和紫色的激光,杯底光斑位置如图丙所示,则
(4) 根据小明的操作和计算结果,小华认为,应该将“偏折比”定义为“光线在空气中与法线的夹角 $ \alpha $ 和光线在其他介质中与法线的夹角 $ \beta $ 之比”。经过对多组不同玻璃砖的实验,测得数据如下表所示。
| 玻璃砖 | $ A $ | $ B $ | $ C $ |
| 光线在空气中与法线的夹角 $ \alpha $ | $ 30.0^{\circ} $ | $ 45.0^{\circ} $ | $ 60.0^{\circ} $ | $ 30.0^{\circ} $ | $ 45.0^{\circ} $ | $ 60.0^{\circ} $ | $ 30.0^{\circ} $ | $ 45.0^{\circ} $ | $ 60.0^{\circ} $ |
| 光线在玻璃中与法线的夹角 $ \beta $ | $ 22.0^{\circ} $ | $ 32.0^{\circ} $ | $ 40.5^{\circ} $ | $ 17.0^{\circ} $ | $ 24.4^{\circ} $ | $ 30.4^{\circ} $ | $ 20.0^{\circ} $ | $ 28.9^{\circ} $ | $ 36.3^{\circ} $ |
| $ \frac{\alpha}{\beta} $ | $ 1.36 $ | $ 1.41 $ | $ 1.48 $ | $ 1.76 $ | $ 1.84 $ | $ 1.97 $ | $ 1.50 $ | $ 1.56 $ | $ 1.65 $ |
问题与证据 根据表格中的数据,分析可得:光在空气与另一种透明介质中传播时,对于不同的入射角,“偏折比”
2024·南通海门区月考
如图甲所示,小明和小华在探究光的折射现象时,将一束入射角为 $ 50^{\circ} $ 的光斜射入杯中的水里,更换杯中的介质时他们发现光的偏折程度不同。为了定量反映这种差异,小明将“折射角与入射角的比值”定义为“偏折比”,并根据所学物理知识和生活经验,对影响“偏折比”大小的因素提出以下猜想:

猜想 1:“偏折比”与液面的高度有关。
猜想 2:“偏折比”与液体的种类有关。
猜想 3:“偏折比”与入射光的颜色有关。
(1) 小华认为猜想 1 是错误的,其理由是
光的折射角与液面高度无关
。根据小明的定义,图甲实验中,测得折射角为 $ 40^{\circ} $,则此时的“偏折比”为0.8
。(2) 为了验证猜想 2,小明只将图甲中的水换成油。如图乙所示,油的高度小于水的高度,杯底光斑的位置恰与图甲实验时光斑的位置重合,对比可知:在相同条件下,油对光的“偏折比”
大于
(填“大于”“等于”或“小于”)水对光的“偏折比”。(3) 为了探究猜想 3,小明用图甲装置先后射入绿色和紫色的激光,杯底光斑位置如图丙所示,则
紫
光的“偏折比”大。将其中的一束激光穿过如图丁所示的玻璃砖,若光在玻璃砖上表面折射时的“偏折比”为 $ 0.8 $,则光在下表面折射时的“偏折比”为1.25
。(4) 根据小明的操作和计算结果,小华认为,应该将“偏折比”定义为“光线在空气中与法线的夹角 $ \alpha $ 和光线在其他介质中与法线的夹角 $ \beta $ 之比”。经过对多组不同玻璃砖的实验,测得数据如下表所示。
| 玻璃砖 | $ A $ | $ B $ | $ C $ |
| 光线在空气中与法线的夹角 $ \alpha $ | $ 30.0^{\circ} $ | $ 45.0^{\circ} $ | $ 60.0^{\circ} $ | $ 30.0^{\circ} $ | $ 45.0^{\circ} $ | $ 60.0^{\circ} $ | $ 30.0^{\circ} $ | $ 45.0^{\circ} $ | $ 60.0^{\circ} $ |
| 光线在玻璃中与法线的夹角 $ \beta $ | $ 22.0^{\circ} $ | $ 32.0^{\circ} $ | $ 40.5^{\circ} $ | $ 17.0^{\circ} $ | $ 24.4^{\circ} $ | $ 30.4^{\circ} $ | $ 20.0^{\circ} $ | $ 28.9^{\circ} $ | $ 36.3^{\circ} $ |
| $ \frac{\alpha}{\beta} $ | $ 1.36 $ | $ 1.41 $ | $ 1.48 $ | $ 1.76 $ | $ 1.84 $ | $ 1.97 $ | $ 1.50 $ | $ 1.56 $ | $ 1.65 $ |
问题与证据 根据表格中的数据,分析可得:光在空气与另一种透明介质中传播时,对于不同的入射角,“偏折比”
不相等
(填“相等”或“不相等”);对于相同的入射角,“偏折比”越大,介质对光的折射程度越高
(填“高”或“低”),因此我们认为小华对“偏折比”定义的优点是能定量反映介质对光的折射程度
。
答案:
(1) 光的折射角与液面高度无关;0.8
(2) 大于
(3) 紫;1.25
(4) 不相等;高;能定量反映介质对光的折射程度
(1) 光的折射角与液面高度无关;0.8
(2) 大于
(3) 紫;1.25
(4) 不相等;高;能定量反映介质对光的折射程度
查看更多完整答案,请扫码查看


