第120页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
14. [2024·武汉经开区期中]高速公路上常用超声波测速仪(位置固定不动)来测量汽车的速度(如图甲所示)。某次检测时,测速仪第一次发出的超声波信号到测速仪接收到经汽车反射回来的超声波信号,用时0.4s;第二次发出信号到测速仪接收到经汽车反射回来的超声波信号,用时0.2s;两次发出信号的时间间隔是1.1s。(超声波在空气中的传播速度为340m/s,汽车保持相同的速度向测速仪方向做直线运动)
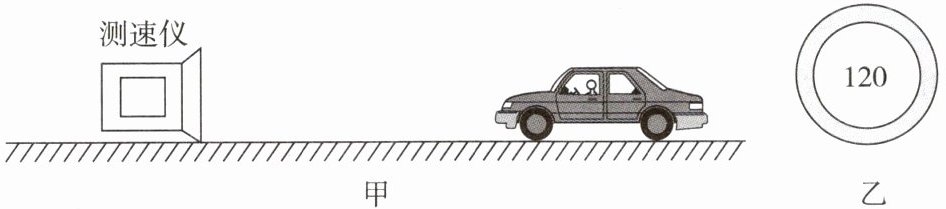
(1)被测汽车第一次遇到超声波时,汽车到超声波测速仪的距离为
(2)被测汽车的速度是

(1)被测汽车第一次遇到超声波时,汽车到超声波测速仪的距离为
68
m。(2)被测汽车的速度是
34
m/s;根据交通标志牌(如图乙所示)判断,被测汽车此时超速
(填“超速”或“未超速”)。
答案:
(1) 第一次超声波往返时间为0.4s,单程时间$t_1=\frac{0.4s}{2}=0.2s$,距离$s_1=v_{声}t_1=340m/s×0.2s=68m$。
(2) 第二次超声波往返时间为0.2s,单程时间$t_2=\frac{0.2s}{2}=0.1s$,距离$s_2=v_{声}t_2=340m/s×0.1s=34m$。汽车行驶距离$\Delta s=s_1-s_2=68m-34m=34m$。两次发出信号间隔1.1s,第一次相遇时刻$t_1'=0.2s$,第二次相遇时刻$t_2'=1.1s+0.1s=1.2s$,时间间隔$\Delta t=t_2'-t_1'=1.2s-0.2s=1s$。汽车速度$v=\frac{\Delta s}{\Delta t}=\frac{34m}{1s}=34m/s=122.4km/h$,大于120km/h,超速。
(1) 68
(2) 34;超速
(1) 第一次超声波往返时间为0.4s,单程时间$t_1=\frac{0.4s}{2}=0.2s$,距离$s_1=v_{声}t_1=340m/s×0.2s=68m$。
(2) 第二次超声波往返时间为0.2s,单程时间$t_2=\frac{0.2s}{2}=0.1s$,距离$s_2=v_{声}t_2=340m/s×0.1s=34m$。汽车行驶距离$\Delta s=s_1-s_2=68m-34m=34m$。两次发出信号间隔1.1s,第一次相遇时刻$t_1'=0.2s$,第二次相遇时刻$t_2'=1.1s+0.1s=1.2s$,时间间隔$\Delta t=t_2'-t_1'=1.2s-0.2s=1s$。汽车速度$v=\frac{\Delta s}{\Delta t}=\frac{34m}{1s}=34m/s=122.4km/h$,大于120km/h,超速。
(1) 68
(2) 34;超速
15.(科学思维·科学推理)地震的发生往往具有突发性。某地发生地震时,震源处同时产生并向各个方向发出P波和S波,P波的传播速度是$7×10^3m/s,S$波的传播速度是$3.5×10^3m/s,$该市地震局于当日21h46min07s探测到P波,于当日21h46min09s探测到S波,则:
(1)地震局距离震源有多远?
(2)震源发生地震的时刻?
]
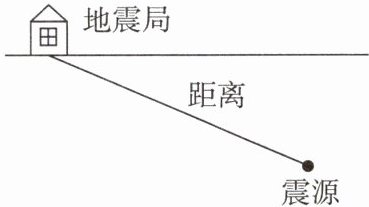
(1)地震局距离震源有多远?
(2)震源发生地震的时刻?
]

答案:
(1)设地震局距离震源的距离为$s$,
由$v = \frac{s}{t}$得,$P$波传播的时间$t_{P} = \frac{s}{v_{P}}$,$S$波传播的时间$t_{S} = \frac{s}{v_{S}}$,
已知$t_{S} - t_{P} = 21h46min09s - 21h46min07s = 2s$,
即$\frac{s}{v_{S}} - \frac{s}{v_{P}} = 2s$,
代入数据$\frac{s}{3.5×10^{3}m/s} - \frac{s}{7×10^{3}m/s} = 2s$,
解得$s = 1.4×10^{4}m$。
(2)$P$波传播的时间$t_{P} = \frac{s}{v_{P}} = \frac{1.4×10^{4}m}{7×10^{3}m/s} = 2s$,
震源发生地震的时刻为$21h46min07s - 2s = 21h46min05s$。
综上,答案为:(1)$1.4×10^{4}m$;(2)$21h46min05s$。
由$v = \frac{s}{t}$得,$P$波传播的时间$t_{P} = \frac{s}{v_{P}}$,$S$波传播的时间$t_{S} = \frac{s}{v_{S}}$,
已知$t_{S} - t_{P} = 21h46min09s - 21h46min07s = 2s$,
即$\frac{s}{v_{S}} - \frac{s}{v_{P}} = 2s$,
代入数据$\frac{s}{3.5×10^{3}m/s} - \frac{s}{7×10^{3}m/s} = 2s$,
解得$s = 1.4×10^{4}m$。
(2)$P$波传播的时间$t_{P} = \frac{s}{v_{P}} = \frac{1.4×10^{4}m}{7×10^{3}m/s} = 2s$,
震源发生地震的时刻为$21h46min07s - 2s = 21h46min05s$。
综上,答案为:(1)$1.4×10^{4}m$;(2)$21h46min05s$。
16. “五一”假期,小明一家驾车外出旅游。一路上,所学的运动学知识帮助他解决了不少实际问题。
(1)经过某交通标志牌时,小明注意到了牌上的标志如图所示。若小明爸爸驾车通过这段路程用时30min,则汽车的速度为多少?
(2)在遵守交通规则的前提下,试计算从标志牌处到上桥最快要用几分钟?
(3)(科学思维·逆向思维)当汽车行至某高速公路入口处时,小明注意到这段高速公路全长180km,行驶速度要求为最低限速60km/h,最高限速120km/h。小明看表此时正好是上午10:00,他很快算出并告诉爸爸要跑完这段路程,必须在哪一段时间到达高速公路出口才不会违规。请你通过计算说明小明告诉爸爸的是哪一段时间。
]
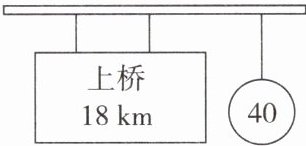
(1)经过某交通标志牌时,小明注意到了牌上的标志如图所示。若小明爸爸驾车通过这段路程用时30min,则汽车的速度为多少?
(2)在遵守交通规则的前提下,试计算从标志牌处到上桥最快要用几分钟?
(3)(科学思维·逆向思维)当汽车行至某高速公路入口处时,小明注意到这段高速公路全长180km,行驶速度要求为最低限速60km/h,最高限速120km/h。小明看表此时正好是上午10:00,他很快算出并告诉爸爸要跑完这段路程,必须在哪一段时间到达高速公路出口才不会违规。请你通过计算说明小明告诉爸爸的是哪一段时间。
]

答案:
(1)36km/h;
(2)27min;
(3)11:30至13:00。
(1)36km/h;
(2)27min;
(3)11:30至13:00。
查看更多完整答案,请扫码查看


