《2025年新课堂同步学习与探究六年级数学上册青岛版》

怎样计算分数除法？
列方程解决有关分数的实际问题时是怎样分析数量关系的？举例子说一说。

答案： 计算分数除法：除以一个数（0除外），等于乘这个数的倒数。
列方程解决有关分数的实际问题分析数量关系：先找出单位“1”的量，设为未知数$x$，根据“单位‘1’的量×对应分率=对应量”的等量关系列方程。
例子：小明有一些零花钱，花了$\frac{2}{5}$后还剩30元，求小明原来有多少零花钱？
分析：单位“1”是小明原来的零花钱，设为$x$元，花了$\frac{2}{5}$，则剩下的分率为$1 - \frac{2}{5} = \frac{3}{5}$，等量关系为原来的零花钱×剩下的分率=剩下的钱数，列方程为$x×(1 - \frac{2}{5}) = 30$。

1. 先在长方形中涂色表示$\frac{6}{7}$，再按下面的算式分一分，并写出得数。

$\frac{6}{7}÷2=$

答案：
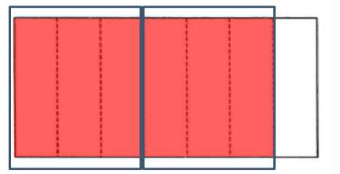
1. $\frac {3} {7}$ 

2. 想一想，填一填。
$(\quad)×5=\frac{1}{2}$ $(\quad)×2=\frac{4}{5}$ $4×(\quad)=\frac{1}{4}$
$\frac{2}{3}÷3=\frac{2}{3}×\frac{(\quad)}{(\quad)}=(\quad)$ $\frac{2}{7}÷6=\frac{2}{7}×\frac{(\quad)}{(\quad)}=(\quad)$

答案： 2. $\frac {1} {10}$ $\frac {2} {5}$ $\frac {1} {16}$ $\frac {1} {3}$ $\frac {2} {9}$ $\frac {1} {6}$ $\frac {1} {21}$

3. 解方程。
$12x=\frac{4}{5}$ $4x=\frac{5}{7}$

答案： 3.  $x = \frac {1} {15}$ $x = \frac {5} {28}$