《2025年新课堂同步学习与探究五年级数学上学期青岛版》

*6. 按要求填写表格后,再想一想。

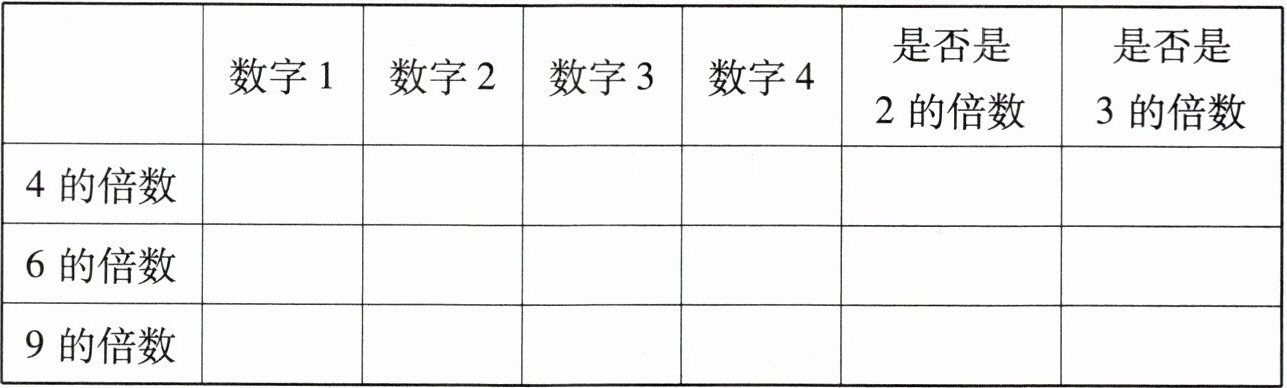
仔细观察表格,你有什么发现？

答案：

如果一个数是4的倍数,那么它一定是2的倍数。如果一个数是6的倍数,那么它一定是2,3的倍数。如果一个数是9的倍数,那么它一定是3的倍数。(答案不唯一。)

- 什么叫质数？什么叫合数？请举例说明。

答案： 质数：一个数，如果只有1和它本身两个因数，这样的数叫做质数（或素数）。举例：2（因数：1、2）、3（因数：1、3）、5（因数：1、5）。
合数：一个数，如果除了1和它本身还有别的因数，这样的数叫做合数。举例：4（因数：1、2、4）、6（因数：1、2、3、6）、8（因数：1、2、4、8）。

- 除0外,按照因数个数的多少可以把自然数分成几类？

答案： 除0外，按照因数个数的多少可以把自然数分成三类：
1. 只有1个因数的数：1；
2. 只有1和它本身两个因数的数：质数；
3. 除了1和它本身还有其他因数的数：合数。
结论：三类。

- 怎样分解质因数？举例说明。
注意：用短除法分解质因数,要记住除数和最后的商都得是质数哟！

答案： 分解质因数是把一个合数用质数相乘的形式表示出来。步骤：用短除法，从最小质数除起，除到商是质数为止，除数和商连乘即为结果。

(1) 在 $1 \sim 20$ 中,最小的质数是(2),最大的合数是(20)。

答案： 2 20

(2) 质数只有(2)个因数,它们分别是(1)和(它本身)。

答案： 2 1 它本身

(3) $15$ 的因数有(1、3、5、15),在这些数中,质数有(3、5),合数有(15)。

答案： 1、3、5、15 3、5 15

(4) 一个自然数的最大因数是 $36$,这个数是(36)。

答案： 36