《2025年新课堂同步学习与探究五年级数学上学期青岛版》

- 等式的性质是什么？举例说明。

答案： 等式的性质有以下两条：
性质1：等式两边加上或减去同一个数，左右两边仍然相等。
例如：若$a = b$，那么$a \pm c = b \pm c$。比如$5 = 5$，$5+3 = 5+3$，即$8 = 8$；$5 - 2=5 - 2$，即$3 = 3$。
性质2：等式两边乘同一个数，或除以同一个不为$0$的数，左右两边仍然相等。
例如：若$a = b$，那么$a× c = b× c$，$a÷ c = b÷ c$（$c\neq0$）。比如$3×4 = 12$，$(3×2)×(4×2)=6×8 = 48$，$12×2×2 = 48$；$10÷2 = 5$，$(10÷2)÷(2÷2)=5÷1 = 5$。

- 利用等式的性质解方程要注意什么？

答案： 利用等式的性质解方程时，要注意等式两边同时加上（或减去）同一个数；同时乘（或除以）同一个不为0的数。

1. 看图填空。

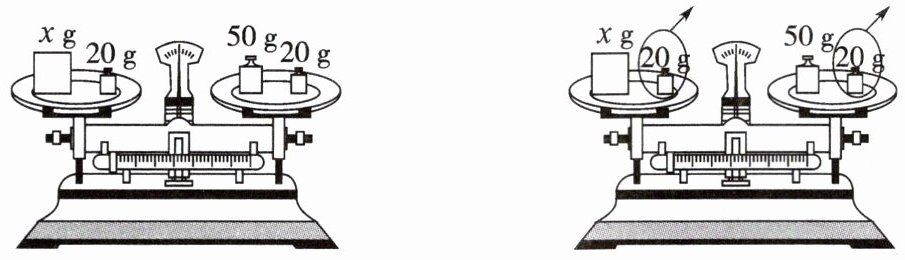
$x + 20 ◯ 70$
$x + 20 - (\quad) ◯ 70 - (\quad)$
$x + 20$=$70$
$x + 20 -$20=$70 -$20

答案： = 20 = 20

2. 解方程。(带“*”的要验算。)
$30 + x = 30$
$*x + 5.2 = 10$

答案： x=0 x=4.8

3. 小明去年身高是多少?

答案： 解:设小明去年身高是x厘米。 x+8=152 x=144