第37页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 你知道什么是方程吗?举例说明。
答案:
答:含有未知数的等式就是方程。
例如:$x + 2 = 5$,$3y = 9$ 。
例如:$x + 2 = 5$,$3y = 9$ 。
- 方程和等式有什么联系和区别?


答案:
1. 联系:
方程都是等式,等式包含方程,方程是等式中的特殊情况。
2. 区别:
等式是表示两个数或者两个表达式之间用等号连接的式子,例如$3 + 2 = 5$,$2x+3=7$(此时是方程,也属于等式),只要是用等号表示相等关系的式子都是等式。
方程是含有未知数的等式,例如$2x + 5 = 15$,方程必须同时满足两个条件:一是等式,二是含有未知数。
方程都是等式,等式包含方程,方程是等式中的特殊情况。
2. 区别:
等式是表示两个数或者两个表达式之间用等号连接的式子,例如$3 + 2 = 5$,$2x+3=7$(此时是方程,也属于等式),只要是用等号表示相等关系的式子都是等式。
方程是含有未知数的等式,例如$2x + 5 = 15$,方程必须同时满足两个条件:一是等式,二是含有未知数。
1. 下面的式子是方程的打“√”。
$7 + x = 35$ (
$8n$ ( ) $4x + 7$ ( )
$13 × 5 = 45$ ( ) $x + 5 < 58$ ( )
$3x = 0$ (
$7 + x = 35$ (
√
) $10 ÷ m = 5$ (√
)$8n$ ( ) $4x + 7$ ( )
$13 × 5 = 45$ ( ) $x + 5 < 58$ ( )
$3x = 0$ (
√
) $4n + 6n = 90$ (√
)
答案:
$7 + x = 35$ ( √ )
$10 ÷ m = 5$ ( √ )
$3x = 0$ ( √ )
$4n + 6n = 90$ ( √ )
$10 ÷ m = 5$ ( √ )
$3x = 0$ ( √ )
$4n + 6n = 90$ ( √ )
2. 看图列方程。
(1)
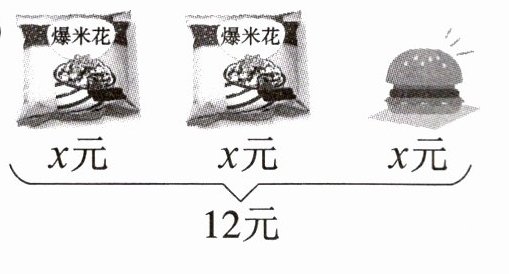
方程:
(2)
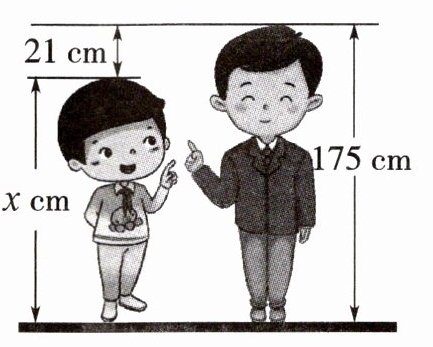
方程:
(3)
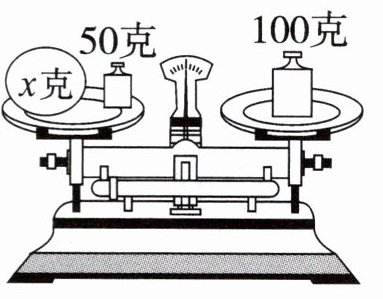
方程:
(4)

方程:
(1)

方程:
(2)

方程:
(3)

方程:
(4)

方程:
答案:
(1)3x=11
(2)x+21=175
(3)x+50=100
(4)2b+15=100
(1)3x=11
(2)x+21=175
(3)x+50=100
(4)2b+15=100
查看更多完整答案,请扫码查看


