《2025年同步测控优化设计八年级数学上册人教版》

3. 计算 $2017×1983 = $3999711.

答案： 3999711

4. 计算：
(1)$\left(-2x^{2} + \dfrac{1}{2}\right)\left(-2x^{2} - \dfrac{1}{2}\right)$；
(2)$\left(\dfrac{1}{2}x^{2}y^{2} + 3m\right)\left(-3m + \dfrac{1}{2}x^{2}y^{2}\right)$；
(3)$9.6×10.4$.

答案： 解（1）$(-2x^{2}+\frac{1}{2})(-2x^{2}-\frac{1}{2})$
$=(-2x^{2})^{2}-(\frac{1}{2})^{2}$
$=4x^{4}-\frac{1}{4}$.
（2）$(\frac{1}{2}x^{2}y^{2}+3m)(-3m+\frac{1}{2}x^{2}y^{2})$
$=(\frac{1}{2}x^{2}y^{2})^{2}-(3m)^{2}$
$=\frac{1}{4}x^{4}y^{4}-9m^{2}$.
（3）$9.6×10.4=(10-0.4)(10+0.4)=100-0.16=99.84$.

5. 如图,圆环形绿地的面积为$400\pi$$m^{2}$(结果保留$\pi$).

答案： $400\pi$ 解析 圆环形绿地的面积为$\pi×25^{2}-\pi×15^{2}=\pi(25+15)(25-15)=400\pi(m^{2})$.

6. 计算：
(1)$2026^{2} - 2025×2027$；
(2)$\left(\dfrac{1}{3}x + y\right)\left(\dfrac{1}{3}x - y\right)\left(\dfrac{1}{9}x^{2} + y^{2}\right)$；
(3)$(-3x - 2y)(2y - 3x) - (5y - 3x)\cdot(3x + 5y)$.

答案： 解（1）$2026^{2}-2025×2027$
$=2026^{2}-(2026-1)×(2026+1)$
$=2026^{2}-(2026^{2}-1)$
$=2026^{2}-2026^{2}+1$
$=1$.
（2）$(\frac{1}{3}x+y)(\frac{1}{3}x-y)(\frac{1}{9}x^{2}+y^{2})$
$=(\frac{1}{9}x^{2}-y^{2})(\frac{1}{9}x^{2}+y^{2})$
$=\frac{1}{81}x^{4}-y^{4}$.
（3）$(-3x-2y)(2y-3x)-(5y-3x)(3x+5y)$
$=9x^{2}-4y^{2}-25y^{2}+9x^{2}$
$=18x^{2}-29y^{2}$.

7. (1)计算下列算式：

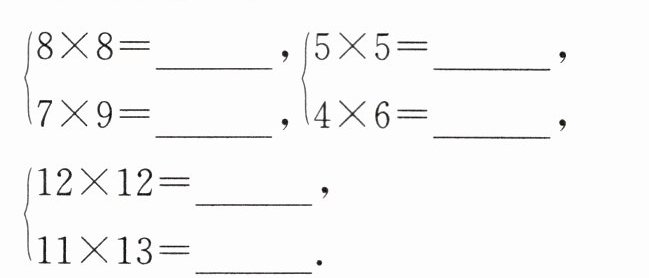
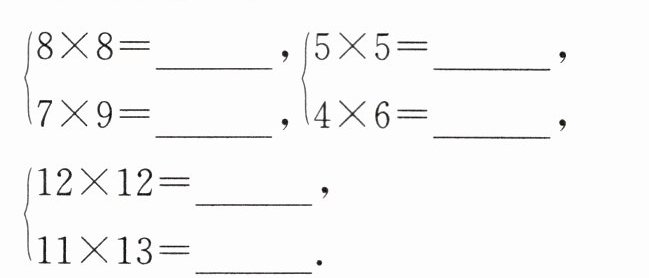
(2)从以上的过程中,你发现了什么规律？请用字母表示出来.
(3)请用你学过的数学知识说明你发现的规律的正确性.
解（1）计算可得
$\begin{cases}8×8=64,\\7×9=63,\end{cases}\begin{cases}5×5=25,\\4×6=24,\end{cases}\begin{cases}12×12=144,\\11×13=143.\end{cases}$
（2）$(n-1)(n+1)=n^{2}-1$.
（3）由平方差公式$(a+b)(a-b)=a^{2}-b^{2}$可知，
当$a=n$，$b=1$时，有$(n-1)(n+1)=n^{2}-1$成立.

答案： 解（1）计算可得
$\begin{cases}8×8=64,\\7×9=63,\end{cases}\begin{cases}5×5=25,\\4×6=24,\end{cases}\begin{cases}12×12=144,\\11×13=143.\end{cases}$
（2）$(n-1)(n+1)=n^{2}-1$.
（3）由平方差公式$(a+b)(a-b)=a^{2}-b^{2}$可知，
当$a=n$，$b=1$时，有$(n-1)(n+1)=n^{2}-1$成立.