第68页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
1. 利用轴对称解决最短路径问题
在直线 $ l $ 的同侧有两个点,在直线 $ l $ 上有到这两个点的距离之和最短的点存在,可以利用
在直线 $ l $ 的同侧有两个点,在直线 $ l $ 上有到这两个点的距离之和最短的点存在,可以利用
轴对称
来确定。
答案:
轴对称
2. 利用平移解决最短路径问题
在画最短路径问题的过程中,若两个点出现在平行直线的异侧时,可用
在画最短路径问题的过程中,若两个点出现在平行直线的异侧时,可用
平移
的方法,转化为求直线异侧的两个点到直线上某一点所连线段的和最小的问题。
答案:
平移
典例 1 如图,某大型农场拟在公路 $ l $ 旁修建一个农产品储藏加工厂,将该农场两个规模相同的水果生产基地 $ A $,$ B $ 的水果集中进行储藏和技术加工,以提高经济效益。请你在图中标明加工厂所在的位置 $ C $,使 $ A $,$ B $ 两地到储藏加工厂的路程之和最短。(要求:保留作图痕迹,不写作法和证明)
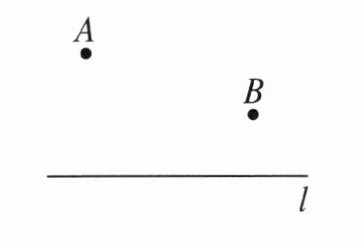

答案:


举一反三 如图,在正方形网格中有 $ M $,$ N $ 两点,在直线 $ l $ 上找一点 $ P $ 使 $ PM+PN $ 最短,则点 $ P $ 应选在(
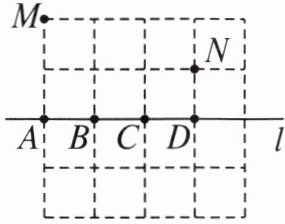
A.$ A $ 点
B.$ B $ 点
C.$ C $ 点
D.$ D $ 点
C
)
A.$ A $ 点
B.$ B $ 点
C.$ C $ 点
D.$ D $ 点
答案:
C
典例 2 如图,从 $ A $ 地到 $ B $ 地要经过一条小河,河的两岸 $ EF // GH $,现要在河上建一座桥(桥垂直于河的两岸),应如何选择桥的位置才能使从 $ A $ 地到 $ B $ 地的路程最短?


答案:


举一反三 如图,直线 $ l_1 $,$ l_2 $ 表示一条河的两岸,且 $ l_1 // l_2 $。现要在这条河上建一座桥(桥与河的两岸相互垂直),使得从村庄 $ P $ 经桥过河到村庄 $ Q $ 的路程最短,应该选择路线( )
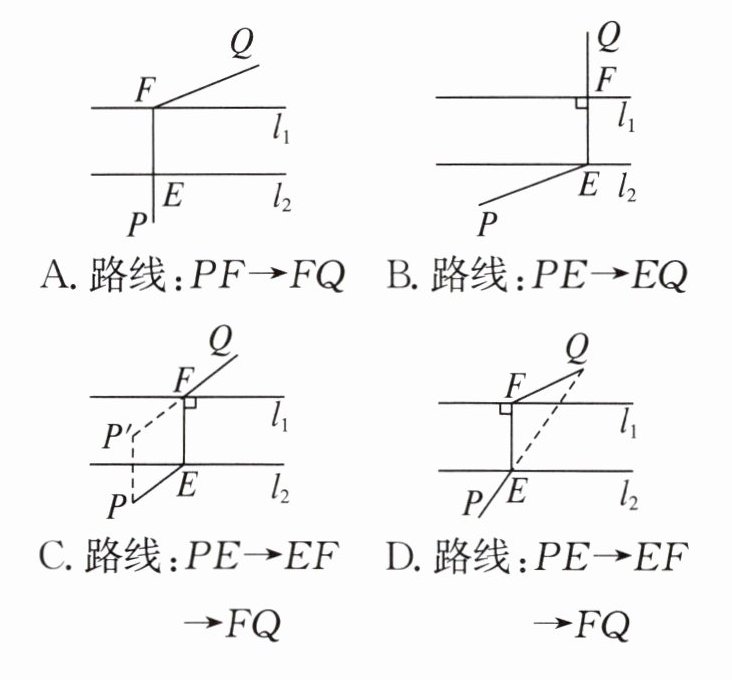

答案:
C
查看更多完整答案,请扫码查看


