《2025年同步测控优化设计八年级数学上册人教版》

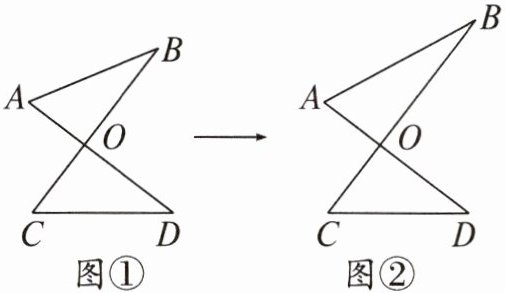
5. 明明在电脑上用画图软件画出的图形如图①,AD与BC交于点O,若他拖动图形,使得∠B的度数减小了6°,∠A的度数增加了6°,得到的图形如图②,设图①中∠C + ∠D的度数为x°,图②中∠C + ∠D的度数为y°,则x与y的数量关系为(A)

A.x = y
B.x = y - 6
C.x = y + 6
D.x = y - 12

答案： A 解析 如题图①，由三角形的内角和定理，得$\angle A+\angle B+\angle AOB=180^{\circ }$，$\angle C+\angle D+\angle COD=180^{\circ }$．$\because \angle AOB=\angle COD$，$\therefore \angle A+\angle B=\angle C+\angle D=x^{\circ }$．如题图②，同理可得$\angle A+\angle B=\angle C+\angle D=y^{\circ }$．$\because \angle B$的度数减小了$6^{\circ }$，$\angle A$的度数增加了$6^{\circ }$，$\therefore \angle A+\angle B$没有发生变化，$\therefore x=y$．故选A．

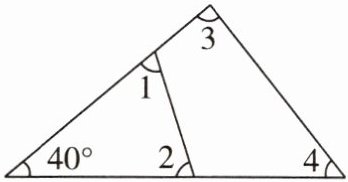
6. 如图,∠1 + ∠2 + ∠3 + ∠4 = $280^{\circ }$。

答案： $280^{\circ }$ 解析 $\because \angle 1+\angle 2=180^{\circ }-40^{\circ }=140^{\circ }$，同理，$\angle 3+\angle 4=140^{\circ }$，$\therefore \angle 1+\angle 2+\angle 3+\angle 4=280^{\circ }$．

7. 某地有A,B,C三个村庄,如图,B村庄在C村庄的正西方向,A村庄在B村庄的北偏东20°方向,同时A村庄又在C村庄的北偏西45°方向,那么∠BAC的度数为多少？

答案： 解 由题意可得$\angle PBC=\angle QCB=90^{\circ }$，$\angle ABC=\angle PBC-\angle PBA=90^{\circ }-20^{\circ }=70^{\circ }$，$\angle ACB=\angle QCB-\angle ACQ=90^{\circ }-45^{\circ }=45^{\circ }$，$\therefore \angle BAC=180^{\circ }-\angle ABC-\angle ACB=180^{\circ }-70^{\circ }-45^{\circ }=65^{\circ }$，$\therefore \angle BAC$的度数是$65^{\circ }$．

8. 当三角形中一个内角α是另一个内角β的两倍时,我们称此三角形为“特征三角形”,其中角α称为“特征角”。
(1) 已知一个“特征三角形”的“特征角”为100°,求这个“特征三角形”最小内角的度数。
(2) 是否存在“特征角”为120°的三角形？若存在,请举例说明；若不存在,请说明理由。

答案： （1）解 设三角形的三个内角分别为$\alpha$，$\beta$，$\gamma$．$\because \alpha =2\beta$，且$\alpha +\beta +\gamma =180^{\circ }$，$\therefore$当$\alpha =100^{\circ }$时，$\beta =50^{\circ }$，则$\gamma =30^{\circ }$，$\therefore$这个“特征三角形”的最小内角的度数为$30^{\circ }$．（2）不存在．$\because \alpha =2\beta$，且$\alpha +\beta +\gamma =180^{\circ }$，$\therefore$当$\alpha =120^{\circ }$时，$\beta =60^{\circ }$，则$\gamma =0^{\circ }$，此时不能构成三角形，故不存在“特征角”为$120^{\circ }$的三角形．