《2025年新课程助学丛书八年级数学上册北师大版》

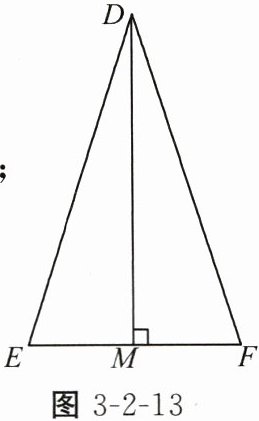
＞ 例1 如图3-2-13,在等腰三角形DEF中,腰$DE= DF= 2\sqrt{10}$,底边$EF= 4$,$DM\perp EF$,交$EF于点M$.
(1)请你在图中建立适当的平面直角坐标系,并写出点$D$,$E$,$F$,$M$的坐标；
(2)解释你选择这个坐标系的理由.
思路提示 可借助等腰三角形的对称性建立平面直角坐标系,或者考虑让特殊点(或边)落在坐标轴上.
尝试解答

小结反思 平面直角坐标系的位置发生改变时,各点对应坐标也会随之发生改变.

答案： 例1
(1)以点M为坐标原点,EF所在直线为x轴,MD所在直线为y轴，建立平面直角坐标系,点M的坐标为(0,0).
∵DE=DF,DM⊥EF,交EF于点M,EF=4,
∴ME=MF=$\frac{1}{2}$EF=2,
∴E(-2,0),F(2,0).
∵在Rt△DEM中,∠DME=90°,DE=2$\sqrt{10}$,ME=2,
∴DM=$\sqrt{DE^2-ME^2}$=6,
∴点D的坐标是(0,6).
(2)理由:选择这个坐标系,所求的点都在坐标轴上,求解简便.

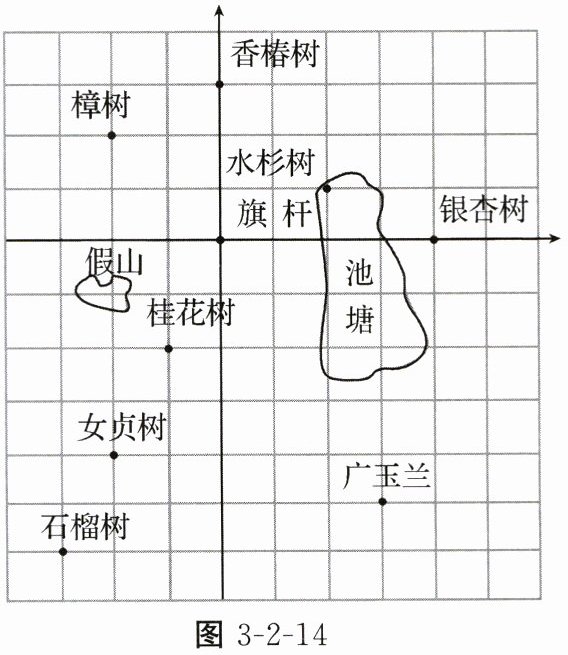
例2 图3-2-14是生物兴趣小组的同学们绘制的校园里部分植物的方位图,为了便于编号,请建立一个适当的平面直角坐标系,并分别写出每种植物的坐标(每个小方格均为边长为1的正方形).
思路提示 建立合理的平面直角坐标系,由点的位置写出坐标.
尝试解答

小结反思 在方格纸上建立平面直角坐标系没有太多的限制要求,只要合理即可.

答案： 解：以旗杆为原点，水平向右为$x$轴正方向，竖直向上为$y$轴正方向建立平面直角坐标系。
则石榴树坐标为$( - 3,-4)$；女贞树坐标为$( - 2,-3)$；桂花树坐标为$( - 1,-2)$；樟树坐标为$( - 2,2)$；香椿树坐标为$(0,3)$；水杉树坐标为$(1,1)$；银杏树坐标为$(4,0)$；广玉兰坐标为$(3,-3)$。