《2025年新课程助学丛书八年级数学上册北师大版》

7. 某校将选拔一名选手参加主题演讲比赛,经研究,按图6 - 1 - 3所示的项目和权重对参赛选手进行考评. 下表是李明、张华在选拔赛中的得分情况：

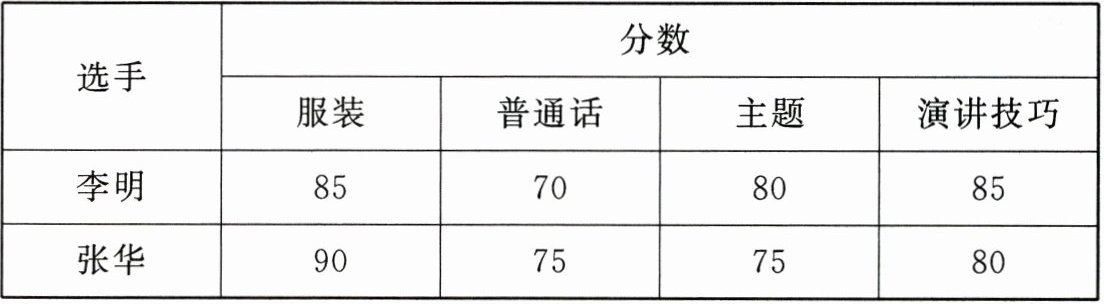
结合以上信息,回答下列问题：

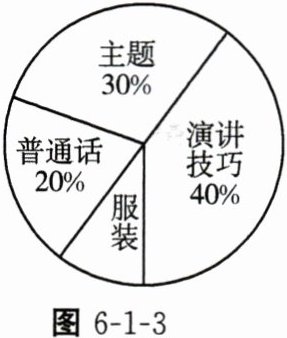
(1)求“服装”项目的权重及“普通话”项目对应的扇形圆心角的度数；
(2)根据所学知识,请你帮助学校在李明和张华两人中选择一人参加主题演讲比赛,并说明理由.

答案： $(1)$ 求“服装”项目的权重及“普通话”项目对应的扇形圆心角的度数
- 求“服装”项目的权重：
因为各项目权重之和为$1$，已知主题权重为$30\%$，普通话权重为$20\%$，演讲技巧权重为$40\%$，所以服装项目的权重为$1 - 30\% - 20\% - 40\%=10\%$。
- 求“普通话”项目对应的扇形圆心角的度数：
根据扇形圆心角公式$\theta = 360^{\circ}×$该部分占总体的百分比，“普通话”项目权重为$20\%$，所以“普通话”项目对应的扇形圆心角的度数为$360^{\circ}×20\% = 72^{\circ}$。
$(2)$ 选择一人参加主题演讲比赛
- 计算李明的综合得分：
根据加权平均数公式$\overline{x}=\sum_{i = 1}^{n}x_{i}w_{i}$（其中$x_{i}$为各项目得分，$w_{i}$为各项目权重）。
李明的综合得分$\overline{x}_{李}=85×10\% + 70×20\% + 80×30\% + 85×40\%$
$=8.5 + 14 + 24 + 34$
$=80.5$（分）。
- 计算张华的综合得分：
张华的综合得分$\overline{x}_{张}=90×10\% + 75×20\% + 75×30\% + 80×40\%$
$=9 + 15 + 22.5 + 32$
$=78.5$（分）。
因为$80.5＞78.5$，即$\overline{x}_{李}＞\overline{x}_{张}$，所以选择李明参加主题演讲比赛，理由是李明的综合得分更高。
综上，$(1)$“服装”项目的权重为$10\%$，“普通话”项目对应的扇形圆心角的度数为$72^{\circ}$；$(2)$选择李明参加，因为李明综合得分$80.5$分高于张华的$78.5$分。

1. 离差平方和是各个数据与它们平均数之差的平方和,即 $ S = $$\sum_{i = 1}^{n}(x_i - \overline{x})^2$。

答案： $S=\sum_{i = 1}^{n}(x_i - \overline{x})^2$

2. 方差是各个数据与平均数之差的平方的平均数,即 $ s^{2} = $$\frac{1}{n}\sum_{i = 1}^{n}(x_{i}-\overline{x})^{2}$（或$\frac{1}{n}\left[(x_{1}-\overline{x})^{2}+(x_{2}-\overline{x})^{2}+\cdots +(x_{n}-\overline{x})^{2}\right]$）(其中,$\overline{x}$ 是 $ x_{1},x_{2},…,x_{n} $ 的平均数)。

答案： $\frac{1}{n}\sum_{i = 1}^{n}(x_{i}-\overline{x})^{2}$（或$\frac{1}{n}\left[(x_{1}-\overline{x})^{2}+(x_{2}-\overline{x})^{2}+\cdots +(x_{n}-\overline{x})^{2}\right]$）

3. 标准差是方差的算术平方根。

答案： 算术平方根

4. 一般而言,一组数据的方差或标准差越小,这组数据就越稳定。

答案： 方差；标准差

例 八(1)班组织了一次食品安全知识竞赛,甲、乙两队各 5 人的成绩(十分制)见下表。

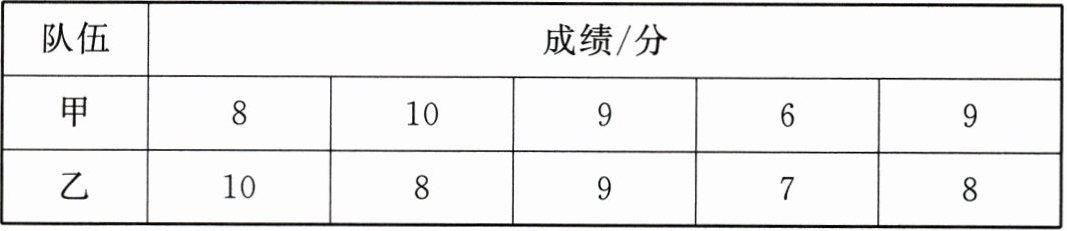
分别计算甲、乙两队的方差,并判断哪队的成绩更稳定,给出判断依据。
思路提示 准确计算平均数,掌握方差的基本公式。
尝试解答
小结反思 方差越小,越稳定。

答案： $s_{甲}^{2}=1.84$，$s_{乙}^{2}=1.04$，$\because s_{甲}^{2}＞s_{乙}^{2}$，$\therefore$乙队的成绩更稳定.