第52页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
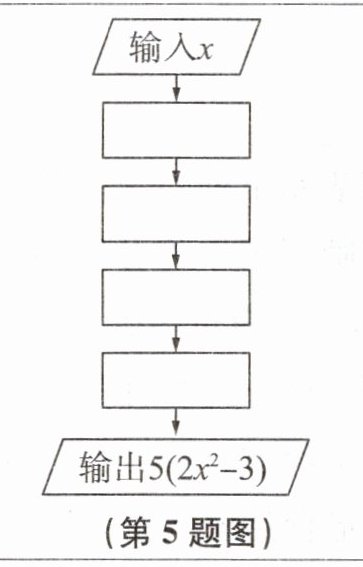
5. 写出右图计算程序的转换步骤,并填写下表:
|输入|$-1$|$-\frac{1}{2}$|$0$|$1.5$|$2$|$\frac{5}{2}$|
|输出|$-5$| | | | | |
6. 如图,在一条数轴上,O为原点,点A,B,C表示的数分别是$m+1$,$2-m$,$9-4m$.
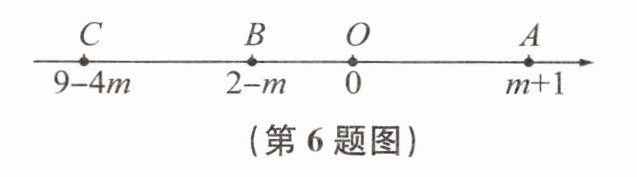
(1)求 AC 的长;(用含m的式子表示)
(2)若$AB= 5$,求 BC 的长.
7. 如图,学校计划在操场主席台前修建一块凹字形花坛.(图中单位:m)
(1)用含a,b的式子表示花坛的面积;
(2)若$a= 4$,$b= 3$,工程费为 500 元/$m^{2}$,求修建花坛的总工程费.
8. 求下列代数式的值.
(1)若$x^{2}+2x= 2$,则代数式$2x^{2}+4x$的值为______;
(2)若代数式$x^{2}+2x+3$的值为 5,求代数式$-2x^{2}-4x+4$的值;
(3)当$x= 1$时,代数式$ax^{3}+bx+4$的值为 7,当$x= -1$时,求代数式$ax^{3}+bx+2$的值.

|输入|$-1$|$-\frac{1}{2}$|$0$|$1.5$|$2$|$\frac{5}{2}$|
|输出|$-5$| | | | | |
6. 如图,在一条数轴上,O为原点,点A,B,C表示的数分别是$m+1$,$2-m$,$9-4m$.

(1)求 AC 的长;(用含m的式子表示)
(2)若$AB= 5$,求 BC 的长.
7. 如图,学校计划在操场主席台前修建一块凹字形花坛.(图中单位:m)
(1)用含a,b的式子表示花坛的面积;
(2)若$a= 4$,$b= 3$,工程费为 500 元/$m^{2}$,求修建花坛的总工程费.
8. 求下列代数式的值.
(1)若$x^{2}+2x= 2$,则代数式$2x^{2}+4x$的值为______;
(2)若代数式$x^{2}+2x+3$的值为 5,求代数式$-2x^{2}-4x+4$的值;
(3)当$x= 1$时,代数式$ax^{3}+bx+4$的值为 7,当$x= -1$时,求代数式$ax^{3}+bx+2$的值.


答案:
5. 假设程序为:输入$x$,计算$3x-2$,输出结果;
|输入|$-1$|$-\frac{1}{2}$|$0$|$1.5$|$2$|$\frac{5}{2}$|
|---|---|---|---|---|---|---|
|输出|$-5$|$-3.5$|$-2$|$2.5$|$4$|$5.5$|
6.
(1) $AC = |9 - 4m - (m + 1)| = |8 - 5m|$;
(2) $AB = |2 - m - (m + 1)| = 5$,
即$|1 - 2m| = 5$,
解得$m = -2$或$m = 3$,
当$m = -2$时,$BC = |9 - 4×(-2) - (2 - (-2))| = 19$;
当$m = 3$时,$BC = |9 - 4×3 - (2 - 3)| = 2$;
7.
(1) 花坛面积$S = 2a^2 + 2ab - b^2$;
(2) 当$a = 4$,$b = 3$时,$S = 2×4^2 + 2×4×3 - 3^2 = 47$,
总工程费为$47 × 500 = 23500$元;
8.
(1) $2x^2 + 4x = 2(x^2 + 2x) = 2 × 2 = 4$;
(2) $x^2 + 2x + 3 = 5$,则$x^2 + 2x = 2$,
$-2x^2 - 4x + 4 = -2(x^2 + 2x) + 4 = -2 × 2 + 4 = 0$;
(3) 当$x = 1$时,$a + b + 4 = 7$,则$a + b = 3$,
当$x = -1$时,$ax^3 + bx + 2 = -a - b + 2 = -3 + 2 = -1$。
|输入|$-1$|$-\frac{1}{2}$|$0$|$1.5$|$2$|$\frac{5}{2}$|
|---|---|---|---|---|---|---|
|输出|$-5$|$-3.5$|$-2$|$2.5$|$4$|$5.5$|
6.
(1) $AC = |9 - 4m - (m + 1)| = |8 - 5m|$;
(2) $AB = |2 - m - (m + 1)| = 5$,
即$|1 - 2m| = 5$,
解得$m = -2$或$m = 3$,
当$m = -2$时,$BC = |9 - 4×(-2) - (2 - (-2))| = 19$;
当$m = 3$时,$BC = |9 - 4×3 - (2 - 3)| = 2$;
7.
(1) 花坛面积$S = 2a^2 + 2ab - b^2$;
(2) 当$a = 4$,$b = 3$时,$S = 2×4^2 + 2×4×3 - 3^2 = 47$,
总工程费为$47 × 500 = 23500$元;
8.
(1) $2x^2 + 4x = 2(x^2 + 2x) = 2 × 2 = 4$;
(2) $x^2 + 2x + 3 = 5$,则$x^2 + 2x = 2$,
$-2x^2 - 4x + 4 = -2(x^2 + 2x) + 4 = -2 × 2 + 4 = 0$;
(3) 当$x = 1$时,$a + b + 4 = 7$,则$a + b = 3$,
当$x = -1$时,$ax^3 + bx + 2 = -a - b + 2 = -3 + 2 = -1$。
5. 写出右图计算程序的转换步骤,并填写下表:
|输入|$-1$|$-\frac{1}{2}$|$0$|$1.5$|$2$|$\frac{5}{2}$|
|输出|$-5$| | | | | |
6. 如图,在一条数轴上,O为原点,点A,B,C表示的数分别是$m+1$,$2-m$,$9-4m$.

(1)求 AC 的长;(用含m的式子表示)
(2)若$AB= 5$,求 BC 的长.
7. 如图,学校计划在操场主席台前修建一块凹字形花坛.(图中单位:m)
(1)用含a,b的式子表示花坛的面积;
(2)若$a= 4$,$b= 3$,工程费为 500 元/$m^{2}$,求修建花坛的总工程费.
8. 求下列代数式的值.
(1)若$x^{2}+2x= 2$,则代数式$2x^{2}+4x$的值为______;
(2)若代数式$x^{2}+2x+3$的值为 5,求代数式$-2x^{2}-4x+4$的值;
(3)当$x= 1$时,代数式$ax^{3}+bx+4$的值为 7,当$x= -1$时,求代数式$ax^{3}+bx+2$的值.


|输入|$-1$|$-\frac{1}{2}$|$0$|$1.5$|$2$|$\frac{5}{2}$|
|输出|$-5$| | | | | |
6. 如图,在一条数轴上,O为原点,点A,B,C表示的数分别是$m+1$,$2-m$,$9-4m$.

(1)求 AC 的长;(用含m的式子表示)
(2)若$AB= 5$,求 BC 的长.
7. 如图,学校计划在操场主席台前修建一块凹字形花坛.(图中单位:m)
(1)用含a,b的式子表示花坛的面积;
(2)若$a= 4$,$b= 3$,工程费为 500 元/$m^{2}$,求修建花坛的总工程费.
8. 求下列代数式的值.
(1)若$x^{2}+2x= 2$,则代数式$2x^{2}+4x$的值为______;
(2)若代数式$x^{2}+2x+3$的值为 5,求代数式$-2x^{2}-4x+4$的值;
(3)当$x= 1$时,代数式$ax^{3}+bx+4$的值为 7,当$x= -1$时,求代数式$ax^{3}+bx+2$的值.


答案:
5. 假设程序为:输入$x$,计算$3x-2$,输出结果。
转换步骤:输入$x$,经过计算$3x - 2$,得到输出值。
当$x = -1$时,$3×(-1)-2=-5$;
当$x = -\frac{1}{2}$时,$3×(-\frac{1}{2})-2=-\frac{7}{2}$;
当$x = 0$时,$3×0 - 2=-2$;
当$x = 1.5$时,$3×1.5-2 = 2.5$;
当$x = 2$时,$3×2-2 = 4$;
当$x = \frac{5}{2}$时,$3×\frac{5}{2}-2=\frac{11}{2}$;
填写表格:
|输入|$-1$|$-\frac{1}{2}$|$0$|$1.5$|$2$|$\frac{5}{2}$|
|输出|$-5$|$-\frac{7}{2}$|$-2$|$2.5$|$4$|$\frac{11}{2}$|
6.
(1)点$A$,$C$表示的数分别是$m + 1$,$9 - 4m$,$AC=\vert(9 - 4m)-(m + 1)\vert=\vert8 - 5m\vert$。
(2)点$A$,$B$表示的数分别是$m + 1$,$2 - m$,$AB=\vert(2 - m)-(m + 1)\vert=\vert1 - 2m\vert$。
因为$AB = 5$,所以$\vert1 - 2m\vert = 5$,则$1 - 2m = 5$或$1 - 2m = -5$。
当$1 - 2m = 5$时,$m = -2$;当$1 - 2m = -5$时,$m = 3$。
点$B$,$C$表示的数分别是$2 - m$,$9 - 4m$,$BC=\vert(9 - 4m)-(2 - m)\vert=\vert7 - 3m\vert$。
当$m = -2$时,$BC=\vert7 - 3×(-2)\vert = 13$;
当$m = 3$时,$BC=\vert7 - 3×3\vert = 2$。
7.
(1)花坛面积$S = 2a(a + b)+ab=2a^{2}+2ab + ab=2a^{2}+3ab$。
(2)当$a = 4$,$b = 3$时,$S=2×4^{2}+3×4×3=32 + 36 = 68$,总工程费为$68×500 = 34000$元。
8.
(1)因为$x^{2}+2x = 2$,所以$2x^{2}+4x=2(x^{2}+2x)=2×2 = 4$。
(2)因为$x^{2}+2x + 3 = 5$,所以$x^{2}+2x = 2$,则$-2x^{2}-4x + 4=-2(x^{2}+2x)+4=-2×2 + 4 = 0$。
(3)当$x = 1$时,$a + b + 4 = 7$,即$a + b = 3$。
当$x = -1$时,$ax^{3}+bx + 2=-a - b + 2=-(a + b)+2=-3 + 2=-1$。
综上,答案依次为:
5. 转换步骤:输入$x$,计算$3x - 2$,输出结果;表格见上述填写。
6.
(1)$\vert8 - 5m\vert$;
(2)$13$或$2$。
7.
(1)$2a^{2}+3ab$;
(2)$34000$元。
8.
(1)$4$;
(2)$0$;
(3)$-1$。
转换步骤:输入$x$,经过计算$3x - 2$,得到输出值。
当$x = -1$时,$3×(-1)-2=-5$;
当$x = -\frac{1}{2}$时,$3×(-\frac{1}{2})-2=-\frac{7}{2}$;
当$x = 0$时,$3×0 - 2=-2$;
当$x = 1.5$时,$3×1.5-2 = 2.5$;
当$x = 2$时,$3×2-2 = 4$;
当$x = \frac{5}{2}$时,$3×\frac{5}{2}-2=\frac{11}{2}$;
填写表格:
|输入|$-1$|$-\frac{1}{2}$|$0$|$1.5$|$2$|$\frac{5}{2}$|
|输出|$-5$|$-\frac{7}{2}$|$-2$|$2.5$|$4$|$\frac{11}{2}$|
6.
(1)点$A$,$C$表示的数分别是$m + 1$,$9 - 4m$,$AC=\vert(9 - 4m)-(m + 1)\vert=\vert8 - 5m\vert$。
(2)点$A$,$B$表示的数分别是$m + 1$,$2 - m$,$AB=\vert(2 - m)-(m + 1)\vert=\vert1 - 2m\vert$。
因为$AB = 5$,所以$\vert1 - 2m\vert = 5$,则$1 - 2m = 5$或$1 - 2m = -5$。
当$1 - 2m = 5$时,$m = -2$;当$1 - 2m = -5$时,$m = 3$。
点$B$,$C$表示的数分别是$2 - m$,$9 - 4m$,$BC=\vert(9 - 4m)-(2 - m)\vert=\vert7 - 3m\vert$。
当$m = -2$时,$BC=\vert7 - 3×(-2)\vert = 13$;
当$m = 3$时,$BC=\vert7 - 3×3\vert = 2$。
7.
(1)花坛面积$S = 2a(a + b)+ab=2a^{2}+2ab + ab=2a^{2}+3ab$。
(2)当$a = 4$,$b = 3$时,$S=2×4^{2}+3×4×3=32 + 36 = 68$,总工程费为$68×500 = 34000$元。
8.
(1)因为$x^{2}+2x = 2$,所以$2x^{2}+4x=2(x^{2}+2x)=2×2 = 4$。
(2)因为$x^{2}+2x + 3 = 5$,所以$x^{2}+2x = 2$,则$-2x^{2}-4x + 4=-2(x^{2}+2x)+4=-2×2 + 4 = 0$。
(3)当$x = 1$时,$a + b + 4 = 7$,即$a + b = 3$。
当$x = -1$时,$ax^{3}+bx + 2=-a - b + 2=-(a + b)+2=-3 + 2=-1$。
综上,答案依次为:
5. 转换步骤:输入$x$,计算$3x - 2$,输出结果;表格见上述填写。
6.
(1)$\vert8 - 5m\vert$;
(2)$13$或$2$。
7.
(1)$2a^{2}+3ab$;
(2)$34000$元。
8.
(1)$4$;
(2)$0$;
(3)$-1$。
5. 写出右图计算程序的转换步骤,并填写下表:
|输入|$-1$|$-\frac{1}{2}$|$0$|$1.5$|$2$|$\frac{5}{2}$|
|输出|$-5$| | | | | |
6. 如图,在一条数轴上,O为原点,点A,B,C表示的数分别是$m+1$,$2-m$,$9-4m$.

(1)求 AC 的长;(用含m的式子表示)
(2)若$AB= 5$,求 BC 的长.
7. 如图,学校计划在操场主席台前修建一块凹字形花坛.(图中单位:m)
(1)用含a,b的式子表示花坛的面积;
(2)若$a= 4$,$b= 3$,工程费为 500 元/$m^{2}$,求修建花坛的总工程费.
8. 求下列代数式的值.
(1)若$x^{2}+2x= 2$,则代数式$2x^{2}+4x$的值为______;
(2)若代数式$x^{2}+2x+3$的值为 5,求代数式$-2x^{2}-4x+4$的值;
(3)当$x= 1$时,代数式$ax^{3}+bx+4$的值为 7,当$x= -1$时,求代数式$ax^{3}+bx+2$的值.


|输入|$-1$|$-\frac{1}{2}$|$0$|$1.5$|$2$|$\frac{5}{2}$|
|输出|$-5$| | | | | |
6. 如图,在一条数轴上,O为原点,点A,B,C表示的数分别是$m+1$,$2-m$,$9-4m$.

(1)求 AC 的长;(用含m的式子表示)
(2)若$AB= 5$,求 BC 的长.
7. 如图,学校计划在操场主席台前修建一块凹字形花坛.(图中单位:m)
(1)用含a,b的式子表示花坛的面积;
(2)若$a= 4$,$b= 3$,工程费为 500 元/$m^{2}$,求修建花坛的总工程费.
8. 求下列代数式的值.
(1)若$x^{2}+2x= 2$,则代数式$2x^{2}+4x$的值为______;
(2)若代数式$x^{2}+2x+3$的值为 5,求代数式$-2x^{2}-4x+4$的值;
(3)当$x= 1$时,代数式$ax^{3}+bx+4$的值为 7,当$x= -1$时,求代数式$ax^{3}+bx+2$的值.


答案:
5. 假设计算程序为:输出 = 输入 × 4 - 1(根据$-1×4-1=-5$,推测此程序)
转换步骤:输出值等于输入值乘以4再减去1。
填写表格:
|输入| $-1$ | $-\frac{1}{2}$ | $0$ | $1.5$ | $2$ | $\frac{5}{2}$ |
|----|-------|----------------|-----|-------|-----|-------------|
|输出| $-5$ | $-3$ | $-1$| $5$ | $7$ | $9$ |
6.
(1) $AC = |(9 - 4m) - (m + 1)| = |8 - 5m|$
(2) $AB = |(2 - m) - (m + 1)| = 5$
$|1 - 2m| = 5$
$1 - 2m = 5$ 或 $1 - 2m = -5$
$m = -2$ 或 $m = 3$
当 $m = -2$ 时,$BC = |(9 - 4×(-2)) - (2 - (-2))| = |17 - 4| = 13$
当 $m = 3$ 时,$BC = |(9 - 4×3) - (2 - 3)| = |-3 + 1| = 2$
7.
(1) 花坛面积 $S = a^2 + 2b(a + a - b) = a^2 + 4ab - 2b^2 -b^2+a^2- 2ab+2b^2= 2a^2 + 2ab - b^2$(由图,由两个$a× a$正方形,和两个长为$a$,宽为$b$,以及一个长为$2a-b$,宽为$b$的长方形组成)
(2) 当 $a = 4$,$b = 3$ 时,
$S = 2× 4^2 + 2× 4× 3 - 3^2 = 32 + 24 - 9 = 47$
总工程费 $= 47 × 500 = 23500$ 元
8.
(1) $2x^2 + 4x = 2(x^2 + 2x) = 2 × 2 = 4$
(2) $x^2 + 2x + 3 = 5$
$x^2 + 2x = 2$
$-2x^2 - 4x + 4 = -2(x^2 + 2x) + 4 = -2 × 2 + 4 = 0$
(3) 当 $x = 1$ 时,$ax^3 + bx + 4 = 7$
$a + b + 4 = 7$
$a + b = 3$
当 $x = -1$ 时,$ax^3 + bx + 2 = -a - b + 2 = -3 + 2 = -1$
转换步骤:输出值等于输入值乘以4再减去1。
填写表格:
|输入| $-1$ | $-\frac{1}{2}$ | $0$ | $1.5$ | $2$ | $\frac{5}{2}$ |
|----|-------|----------------|-----|-------|-----|-------------|
|输出| $-5$ | $-3$ | $-1$| $5$ | $7$ | $9$ |
6.
(1) $AC = |(9 - 4m) - (m + 1)| = |8 - 5m|$
(2) $AB = |(2 - m) - (m + 1)| = 5$
$|1 - 2m| = 5$
$1 - 2m = 5$ 或 $1 - 2m = -5$
$m = -2$ 或 $m = 3$
当 $m = -2$ 时,$BC = |(9 - 4×(-2)) - (2 - (-2))| = |17 - 4| = 13$
当 $m = 3$ 时,$BC = |(9 - 4×3) - (2 - 3)| = |-3 + 1| = 2$
7.
(1) 花坛面积 $S = a^2 + 2b(a + a - b) = a^2 + 4ab - 2b^2 -b^2+a^2- 2ab+2b^2= 2a^2 + 2ab - b^2$(由图,由两个$a× a$正方形,和两个长为$a$,宽为$b$,以及一个长为$2a-b$,宽为$b$的长方形组成)
(2) 当 $a = 4$,$b = 3$ 时,
$S = 2× 4^2 + 2× 4× 3 - 3^2 = 32 + 24 - 9 = 47$
总工程费 $= 47 × 500 = 23500$ 元
8.
(1) $2x^2 + 4x = 2(x^2 + 2x) = 2 × 2 = 4$
(2) $x^2 + 2x + 3 = 5$
$x^2 + 2x = 2$
$-2x^2 - 4x + 4 = -2(x^2 + 2x) + 4 = -2 × 2 + 4 = 0$
(3) 当 $x = 1$ 时,$ax^3 + bx + 4 = 7$
$a + b + 4 = 7$
$a + b = 3$
当 $x = -1$ 时,$ax^3 + bx + 2 = -a - b + 2 = -3 + 2 = -1$
5. 写出右图计算程序的转换步骤,并填写下表:
|输入|$-1$|$-\frac{1}{2}$|$0$|$1.5$|$2$|$\frac{5}{2}$|
|输出|$-5$| | | | | |
转换步骤:输入$x$→计算$x^2$→乘以2→减去3→乘以5→输出$5(2x^2 - 3)$。
表格输出:$-\frac{25}{2}$;$-15$;$\frac{15}{2}$;$25$;$\frac{95}{2}$
6. 如图,在一条数轴上,O为原点,点A,B,C表示的数分别是$m+1$,$2-m$,$9-4m$.

(1)求 AC 的长;(用含m的式子表示)
(2)若$AB= 5$,求 BC 的长.
7. 如图,学校计划在操场主席台前修建一块凹字形花坛.(图中单位:m)
(1)用含a,b的式子表示花坛的面积;
(2)若$a= 4$,$b= 3$,工程费为 500 元/$m^{2}$,求修建花坛的总工程费.
8. 求下列代数式的值.
(1)若$x^{2}+2x= 2$,则代数式$2x^{2}+4x$的值为______;
(2)若代数式$x^{2}+2x+3$的值为 5,求代数式$-2x^{2}-4x+4$的值;
(3)当$x= 1$时,代数式$ax^{3}+bx+4$的值为 7,当$x= -1$时,求代数式$ax^{3}+bx+2$的值.


|输入|$-1$|$-\frac{1}{2}$|$0$|$1.5$|$2$|$\frac{5}{2}$|
|输出|$-5$| | | | | |
转换步骤:输入$x$→计算$x^2$→乘以2→减去3→乘以5→输出$5(2x^2 - 3)$。
表格输出:$-\frac{25}{2}$;$-15$;$\frac{15}{2}$;$25$;$\frac{95}{2}$
6. 如图,在一条数轴上,O为原点,点A,B,C表示的数分别是$m+1$,$2-m$,$9-4m$.

(1)求 AC 的长;(用含m的式子表示)
$AC = (m+1) - (9-4m) = 5m - 8$
(2)若$AB= 5$,求 BC 的长.
$AB = (m+1) - (2 - m) = 2m - 1$,由$AB=5$得$2m - 1=5$,解得$m=3$。$BC = (2 - m) - (9 - 4m) = 3m - 7$,代入$m=3$,得$BC=3×3 - 7=2$
7. 如图,学校计划在操场主席台前修建一块凹字形花坛.(图中单位:m)
(1)用含a,b的式子表示花坛的面积;
花坛面积=外围面积-空白面积。外围长$2a + 3b$,宽$2a + b$;空白长$3b$,宽$2a$。面积$=(2a + 3b)(2a + b) - 3b·2a = 4a^2 + 2ab + 3b^2$
(2)若$a= 4$,$b= 3$,工程费为 500 元/$m^{2}$,求修建花坛的总工程费.
当$a=4$,$b=3$时,面积$=4×4^2 + 2×4×3 + 3×3^2=115\,m^2$,总费用$115×500=57500$元
8. 求下列代数式的值.
(1)若$x^{2}+2x= 2$,则代数式$2x^{2}+4x$的值为______;
4
(2)若代数式$x^{2}+2x+3$的值为 5,求代数式$-2x^{2}-4x+4$的值;
由$x^2 + 2x + 3=5$得$x^2 + 2x=2$,$-2x^2 -4x +4=-2(x^2 + 2x)+4=-4 +4=0$
(3)当$x= 1$时,代数式$ax^{3}+bx+4$的值为 7,当$x= -1$时,求代数式$ax^{3}+bx+2$的值.
当$x=1$时,$a + b + 4=7$,则$a + b=3$。当$x=-1$时,$-a -b + 2=-(a + b)+2=-3 +2=-1$


答案:
第5题
转换步骤:输入$x$→计算$x^2$→乘以2→减去3→乘以5→输出$5(2x^2 - 3)$。
表格输出:
$-\frac{25}{2}$;$-15$;$\frac{15}{2}$;$25$;$\frac{95}{2}$
第6题
(1) $AC = (m+1) - (9-4m) = 5m - 8$
(2) $AB = (m+1) - (2 - m) = 2m - 1$,由$AB=5$得$2m - 1=5$,解得$m=3$。
$BC = (2 - m) - (9 - 4m) = 3m - 7$,代入$m=3$,得$BC=3×3 - 7=2$
第7题
(1) 花坛面积=外围面积-空白面积。外围长$2a + 3b$,宽$2a + b$;空白长$3b$,宽$2a$。
面积$=(2a + 3b)(2a + b) - 3b·2a = 4a^2 + 2ab + 3b^2$
(2) 当$a=4$,$b=3$时,面积$=4×4^2 + 2×4×3 + 3×3^2=115\,m^2$,总费用$115×500=57500$元
第8题
(1) $4$
(2) 由$x^2 + 2x + 3=5$得$x^2 + 2x=2$,$-2x^2 -4x +4=-2(x^2 + 2x)+4=-4 +4=0$
(3) 当$x=1$时,$a + b + 4=7$,则$a + b=3$。当$x=-1$时,$-a -b + 2=-(a + b)+2=-3 +2=-1$
转换步骤:输入$x$→计算$x^2$→乘以2→减去3→乘以5→输出$5(2x^2 - 3)$。
表格输出:
$-\frac{25}{2}$;$-15$;$\frac{15}{2}$;$25$;$\frac{95}{2}$
第6题
(1) $AC = (m+1) - (9-4m) = 5m - 8$
(2) $AB = (m+1) - (2 - m) = 2m - 1$,由$AB=5$得$2m - 1=5$,解得$m=3$。
$BC = (2 - m) - (9 - 4m) = 3m - 7$,代入$m=3$,得$BC=3×3 - 7=2$
第7题
(1) 花坛面积=外围面积-空白面积。外围长$2a + 3b$,宽$2a + b$;空白长$3b$,宽$2a$。
面积$=(2a + 3b)(2a + b) - 3b·2a = 4a^2 + 2ab + 3b^2$
(2) 当$a=4$,$b=3$时,面积$=4×4^2 + 2×4×3 + 3×3^2=115\,m^2$,总费用$115×500=57500$元
第8题
(1) $4$
(2) 由$x^2 + 2x + 3=5$得$x^2 + 2x=2$,$-2x^2 -4x +4=-2(x^2 + 2x)+4=-4 +4=0$
(3) 当$x=1$时,$a + b + 4=7$,则$a + b=3$。当$x=-1$时,$-a -b + 2=-(a + b)+2=-3 +2=-1$
9. 观察下列等式:$-1×\frac{1}{2}= -1+\frac{1}{2}$,$-\frac{1}{2}×\frac{1}{3}= -\frac{1}{2}+\frac{1}{3}$,$-\frac{1}{3}×\frac{1}{4}= -\frac{1}{3}+\frac{1}{4}$,…
(1)写出第 4 个等式:
(2)计算:$(-1×\frac{1}{2})+(-\frac{1}{2}×\frac{1}{3})+(-\frac{1}{3}×\frac{1}{4})+…+(-\frac{1}{2023}×\frac{1}{2024})$.
(1)写出第 4 个等式:
$-\frac{1}{4} × \frac{1}{5} = -\frac{1}{4} + \frac{1}{5}$
;(2)计算:$(-1×\frac{1}{2})+(-\frac{1}{2}×\frac{1}{3})+(-\frac{1}{3}×\frac{1}{4})+…+(-\frac{1}{2023}×\frac{1}{2024})$.
$(-1 × \frac{1}{2}) + (-\frac{1}{2} × \frac{1}{3}) + (-\frac{1}{3} × \frac{1}{4}) + \ldots + (-\frac{1}{2023} × \frac{1}{2024})$
$= (-1 + \frac{1}{2}) + (-\frac{1}{2} + \frac{1}{3}) + (-\frac{1}{3} + \frac{1}{4}) + \ldots + (-\frac{1}{2023} + \frac{1}{2024})$
$=-1+\frac{1}{2} - \frac{1}{2} + \frac{1}{3} - \frac{1}{3} + \frac{1}{4} - \ldots - \frac{1}{2023} + \frac{1}{2024}$
$=-1+\frac{1}{2024}$
$=-\frac{2023}{2024}$
$= (-1 + \frac{1}{2}) + (-\frac{1}{2} + \frac{1}{3}) + (-\frac{1}{3} + \frac{1}{4}) + \ldots + (-\frac{1}{2023} + \frac{1}{2024})$
$=-1+\frac{1}{2} - \frac{1}{2} + \frac{1}{3} - \frac{1}{3} + \frac{1}{4} - \ldots - \frac{1}{2023} + \frac{1}{2024}$
$=-1+\frac{1}{2024}$
$=-\frac{2023}{2024}$
答案:
(1)第 4 个等式:$-\frac{1}{4} × \frac{1}{5} = -\frac{1}{4} + \frac{1}{5}$。
(2)
$(-1 × \frac{1}{2}) + (-\frac{1}{2} × \frac{1}{3}) + (-\frac{1}{3} × \frac{1}{4}) + \ldots + (-\frac{1}{2023} × \frac{1}{2024})$
$= (-1 + \frac{1}{2}) + (-\frac{1}{2} + \frac{1}{3}) + (-\frac{1}{3} + \frac{1}{4}) + \ldots + (-\frac{1}{2023} + \frac{1}{2024})$
$=-1+\frac{1}{2} - \frac{1}{2} + \frac{1}{3} - \frac{1}{3} + \frac{1}{4} - \ldots - \frac{1}{2023} + \frac{1}{2024}$
$=-1+\frac{1}{2024}$
$=-\frac{2023}{2024}$
(1)第 4 个等式:$-\frac{1}{4} × \frac{1}{5} = -\frac{1}{4} + \frac{1}{5}$。
(2)
$(-1 × \frac{1}{2}) + (-\frac{1}{2} × \frac{1}{3}) + (-\frac{1}{3} × \frac{1}{4}) + \ldots + (-\frac{1}{2023} × \frac{1}{2024})$
$= (-1 + \frac{1}{2}) + (-\frac{1}{2} + \frac{1}{3}) + (-\frac{1}{3} + \frac{1}{4}) + \ldots + (-\frac{1}{2023} + \frac{1}{2024})$
$=-1+\frac{1}{2} - \frac{1}{2} + \frac{1}{3} - \frac{1}{3} + \frac{1}{4} - \ldots - \frac{1}{2023} + \frac{1}{2024}$
$=-1+\frac{1}{2024}$
$=-\frac{2023}{2024}$
查看更多完整答案,请扫码查看


