《2025年新课程示径学案作业设计七年级数学上册苏科版》

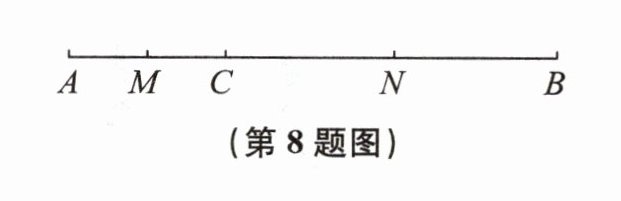
8. 如图,C是线段AB上一点,M是AC的中点,N是BC的中点.
(1) 若AM= 1,BC= 4,求MN的长;
(2) 若AB= 6,求MN的长.

答案：
(1) 3；
(2) 3

9. 如图,已知点B,C在线段AD上,且AB= CD.
(1) 比较线段的大小:AC=BD;(填“＞”“=”或“＜”)
(2) 如果AD= 18,BC= 12,M是AB的中点,N是CD的中点,求线段MN的长度.
(3) 在(2)中,如果AD= a,BC= b,其他条件不变,那么MN=$\frac{a + b}{2}$.(用含a,b的式子表示)

答案： （1）$= $
（2）
因为$AB = CD$，$AD=18$，$BC = 12$，
所以$AB+CD=AD - BC=18 - 12 = 6$，
则$AB=CD = 3$。
$MB=\frac{1}{2}AB=\frac{3}{2}$，$CN=\frac{1}{2}CD=\frac{3}{2}$。
$MN=MB + BC+CN=\frac{3}{2}+12+\frac{3}{2}=15$。
（3）$\frac{a + b}{2}$

10. 如图,M是定长线段AB上一定点,点C以1 cm/s的速度从点M出发.同时,点D以3 cm/s的速度从点B出发,都沿直线BA向左运动(点C在线段AM上,点D在线段BM上).
(1) 若AB= 10 cm,当点C,D运动2 s时,求AC+MD的值;
(2) 若点C,D运动时,总有MD= 3AC,则AM,AB之间的数量关系为AB=4AM;
(3) 在(2)的条件下,N是线段AB上一点,且AN-BN= MN,求$\frac{MN}{AB}$的值.

(1) 设运动时间为$ t=2\,s $，则$ CM=1×2=2\,cm $，$ BD=3×2=6\,cm $。
$\because AC=AM-CM$，$ MD=MB-BD $，
$\therefore AC+MD=(AM-CM)+(MB-BD)=(AM+MB)-(CM+BD)=AB-(2+6) $。
$\because AB=10\,cm$，$\therefore AC+MD=10-8=2\,cm$。
(2) 设运动时间为$ t $，则$ CM=t\,cm $，$ BD=3t\,cm $。
$\because AC=AM-CM=AM-t$，$ MD=MB-BD=MB-3t $，
由$ MD=3AC $得：$ MB-3t=3(AM-t) $，
化简得$ MB=3AM $。
$\because AB=AM+MB$，$\therefore AB=AM+3AM=4AM$，即$ AB=4AM $。
(3) 设$ AM=x $，则$ AB=4x $，$ MB=3x $。设$ N $在数轴上坐标为$ n $（以$ A $为原点，$ AB $方向为正方向），则$ A(0) $，$ B(4x) $，$ M(x) $，$ N(n) $。
$\because AN-BN=MN$，$\therefore n-(4x-n)=|n-x|$，即$ 2n-4x=|n-x| $。
若$ n\geq x $，则$ |n-x|=n-x $，方程为$ 2n-4x=n-x $，解得$ n=3x $。
若$ n＜x $，则$ |n-x|=x-n $，方程为$ 2n-4x=x-n $，解得$ n=\frac{5x}{3} $（与$ n＜x $矛盾，舍去）。
$\therefore N(3x)$，$ MN=3x-x=2x $，$\frac{MN}{AB}=\frac{2x}{4x}=\frac{1}{2}$。
(1) 2 cm
(2) AB=4AM
(3) $\frac{1}{2}$

答案：
(1) 设运动时间为$ t=2\,s $，则$ CM=1×2=2\,cm $，$ BD=3×2=6\,cm $。
$\because AC=AM-CM$，$ MD=MB-BD $，
$\therefore AC+MD=(AM-CM)+(MB-BD)=(AM+MB)-(CM+BD)=AB-(2+6) $。
$\because AB=10\,cm$，$\therefore AC+MD=10-8=2\,cm$。
(2) 设运动时间为$ t $，则$ CM=t\,cm $，$ BD=3t\,cm $。
$\because AC=AM-CM=AM-t$，$ MD=MB-BD=MB-3t $，
由$ MD=3AC $得：$ MB-3t=3(AM-t) $，
化简得$ MB=3AM $。
$\because AB=AM+MB$，$\therefore AB=AM+3AM=4AM$，即$ AB=4AM $。
(3) 设$ AM=x $，则$ AB=4x $，$ MB=3x $。设$ N $在数轴上坐标为$ n $（以$ A $为原点，$ AB $方向为正方向），则$ A(0) $，$ B(4x) $，$ M(x) $，$ N(n) $。
$\because AN-BN=MN$，$\therefore n-(4x-n)=|n-x|$，即$ 2n-4x=|n-x| $。
若$ n\geq x $，则$ |n-x|=n-x $，方程为$ 2n-4x=n-x $，解得$ n=3x $。
若$ n＜x $，则$ |n-x|=x-n $，方程为$ 2n-4x=x-n $，解得$ n=\frac{5x}{3} $（与$ n＜x $矛盾，舍去）。
$\therefore N(3x)$，$ MN=3x-x=2x $，$\frac{MN}{AB}=\frac{2x}{4x}=\frac{1}{2}$。
(1) $ 2\,cm $
(2) $ AB=4AM $
(3) $ \frac{1}{2} $