第126页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
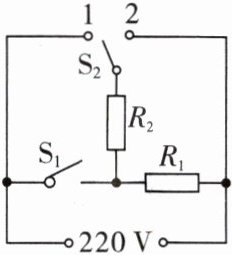
16.(1805,1808)如图所示是某种多功能炖锅的简化电路图。$R_1、$$R_2$是两个电热丝$,S_2$是单刀双掷开关。通过开关$S_1$和$S_2$的闭合、断开的组合,实现高、中、低三挡加热。多功能炖锅的相关参数见表。问:
(1)两个开关分别处于什么状态时,炖锅电路处于低温挡?并说明理由。
(2)炖锅处于低温挡工作6 min消耗多少电能?
(3)电热丝$R_2$的阻值是多少?

(1)两个开关分别处于什么状态时,炖锅电路处于低温挡?并说明理由。
(2)炖锅处于低温挡工作6 min消耗多少电能?
(3)电热丝$R_2$的阻值是多少?


答案:
(1)
当$S_1$断开,$S_2$接$2$时,$R_1$与$R_2$串联,此时电路总电阻$R_{串}=R_1 + R_2$;当$S_1$闭合,$S_2$接$1$时,$R_1$与$R_2$并联,此时电路总电阻$R_{并}=\frac{R_1R_2}{R_1 + R_2}$;当$S_1$闭合,$S_2$接$2$时,只有$R_1$接入电路,此时电路总电阻$R_{1}$。
根据$P = \frac{U^{2}}{R}$($U$为电源电压,$R$为电路总电阻),电源电压$U$不变,串联时总电阻最大,所以功率最小,炖锅电路处于低温挡。
(2)
已知低温挡功率$P_{低}=275W$,工作时间$t = 6min=6×60s = 360s$。
根据$W = P_{低}t$,可得$W=275W×360s = 99000J$。
(3)
当$S_1$闭合,$S_2$接$2$时,只有$R_1$接入电路,此时为中温挡,$P_{中}=550W$,根据$P = \frac{U^{2}}{R}$,可得$R_1=\frac{U^{2}}{P_{中}}=\frac{(220V)^{2}}{550W}=88\Omega$。
当$S_1$闭合,$S_2$接$1$时,$R_1$与$R_2$并联,此时为高温挡,$P_{高}=1100W$,则$P_{2}=P_{高}-P_{中}=1100W - 550W = 550W$。
再根据$P = \frac{U^{2}}{R}$,可得$R_2=\frac{U^{2}}{P_{2}}=\frac{(220V)^{2}}{550W}=88\Omega$。
综上,答案依次为:
(1)$S_1$断开,$S_2$接$2$时处于低温挡,理由是此时$R_1$与$R_2$串联,总电阻最大,根据$P = \frac{U^{2}}{R}$,电源电压不变,功率最小;
(2)$99000J$;
(3)$88\Omega$。
(1)
当$S_1$断开,$S_2$接$2$时,$R_1$与$R_2$串联,此时电路总电阻$R_{串}=R_1 + R_2$;当$S_1$闭合,$S_2$接$1$时,$R_1$与$R_2$并联,此时电路总电阻$R_{并}=\frac{R_1R_2}{R_1 + R_2}$;当$S_1$闭合,$S_2$接$2$时,只有$R_1$接入电路,此时电路总电阻$R_{1}$。
根据$P = \frac{U^{2}}{R}$($U$为电源电压,$R$为电路总电阻),电源电压$U$不变,串联时总电阻最大,所以功率最小,炖锅电路处于低温挡。
(2)
已知低温挡功率$P_{低}=275W$,工作时间$t = 6min=6×60s = 360s$。
根据$W = P_{低}t$,可得$W=275W×360s = 99000J$。
(3)
当$S_1$闭合,$S_2$接$2$时,只有$R_1$接入电路,此时为中温挡,$P_{中}=550W$,根据$P = \frac{U^{2}}{R}$,可得$R_1=\frac{U^{2}}{P_{中}}=\frac{(220V)^{2}}{550W}=88\Omega$。
当$S_1$闭合,$S_2$接$1$时,$R_1$与$R_2$并联,此时为高温挡,$P_{高}=1100W$,则$P_{2}=P_{高}-P_{中}=1100W - 550W = 550W$。
再根据$P = \frac{U^{2}}{R}$,可得$R_2=\frac{U^{2}}{P_{2}}=\frac{(220V)^{2}}{550W}=88\Omega$。
综上,答案依次为:
(1)$S_1$断开,$S_2$接$2$时处于低温挡,理由是此时$R_1$与$R_2$串联,总电阻最大,根据$P = \frac{U^{2}}{R}$,电源电压不变,功率最小;
(2)$99000J$;
(3)$88\Omega$。
17.(1806)直流充电桩是一种为电动汽车补给能量的装置,如图甲所示。它能够将电网中的交流转化为直流,再将电能充入汽车动力电池(以下简称电池)。通常,直流充电桩比交流充电桩的充电电压更高、电流更大,因而可实现快速充电。
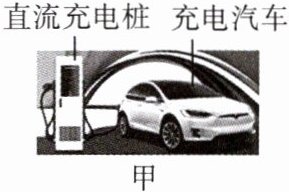
设电池当前储能占充满状态储能的百分比为D。充电时,充电桩的充电功率P会随着电池的D的变化而变化,同时用户还可以通过充电桩显示屏了解充电过程中的其他相关信息。
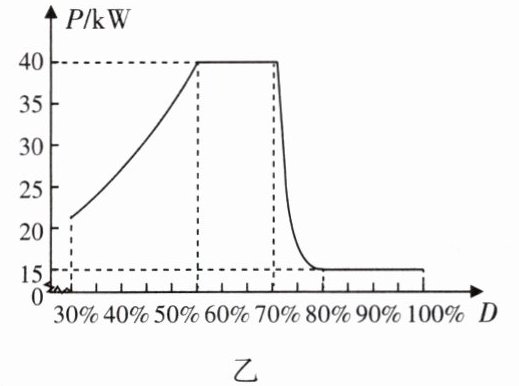
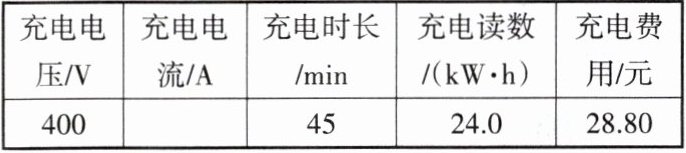
现实际测试一个直流充电桩对某辆电动汽车的充电性能。假定测试中充电桩输出的电能全部转化为电池的储能。充电前,D为30%,充电桩显示屏中充电时长、充电度数、充电费用示数均为0。开始充电后,P与D的关系如图乙所示(为方便计算,图像已作近似处理)。充满后,立即停止充电。当D达到70%时充电桩显示屏的部分即时信息如表所示。
(1)通常,直流充电桩比交流充电桩的充电电压更高、电流更大,故充电功率更
(2)在D从30%增至70%的过程中,充电功率大致的变化规律是
(3)若充电过程中充电电费单价不变,则测试全过程的充电费用多少元?
(4)设D从70%增至80%所需时间为$t_1,$从80%增至90%所需时间为$t_2,$且$t_1:t_2= 2:3,$则充电全过程的总时长为多少分钟?

设电池当前储能占充满状态储能的百分比为D。充电时,充电桩的充电功率P会随着电池的D的变化而变化,同时用户还可以通过充电桩显示屏了解充电过程中的其他相关信息。
现实际测试一个直流充电桩对某辆电动汽车的充电性能。假定测试中充电桩输出的电能全部转化为电池的储能。充电前,D为30%,充电桩显示屏中充电时长、充电度数、充电费用示数均为0。开始充电后,P与D的关系如图乙所示(为方便计算,图像已作近似处理)。充满后,立即停止充电。当D达到70%时充电桩显示屏的部分即时信息如表所示。


(1)通常,直流充电桩比交流充电桩的充电电压更高、电流更大,故充电功率更
大
。(2)在D从30%增至70%的过程中,充电功率大致的变化规律是
先增大后不变
。当D为70%时,充电电流为100
A。(3)若充电过程中充电电费单价不变,则测试全过程的充电费用多少元?
50.4
(4)设D从70%增至80%所需时间为$t_1,$从80%增至90%所需时间为$t_2,$且$t_1:t_2= 2:3,$则充电全过程的总时长为多少分钟?
93
答案:
(1)大
(2)先增大后不变;100
(3)电费单价:$28.80元÷24.0kW\cdot h = 1.2元/(kW\cdot h)$,全过程充电度数:$\frac{70\%}{40\%}×24.0kW\cdot h=42kW\cdot h$,总费用:$42kW\cdot h×1.2元/(kW\cdot h)=50.4元$
(4)总储能$W_{总}=24kW\cdot h÷40\% = 60kW\cdot h$,每10%储能电能$6kW\cdot h$。设$t_1=2k$,$t_2=3k$,90%-100%功率$15kW$,$t_3=6kW\cdot h÷15kW=0.4h=24min$。由70%-80%和80%-90%功率线性变化及$t_1:t_2=2:3$,解得$t_1=9.6min$,$t_2=14.4min$。总时长:$45min+9.6min+14.4min+24min=93min$
(1)大
(2)先增大后不变;100
(3)50.4
(4)93
(1)大
(2)先增大后不变;100
(3)电费单价:$28.80元÷24.0kW\cdot h = 1.2元/(kW\cdot h)$,全过程充电度数:$\frac{70\%}{40\%}×24.0kW\cdot h=42kW\cdot h$,总费用:$42kW\cdot h×1.2元/(kW\cdot h)=50.4元$
(4)总储能$W_{总}=24kW\cdot h÷40\% = 60kW\cdot h$,每10%储能电能$6kW\cdot h$。设$t_1=2k$,$t_2=3k$,90%-100%功率$15kW$,$t_3=6kW\cdot h÷15kW=0.4h=24min$。由70%-80%和80%-90%功率线性变化及$t_1:t_2=2:3$,解得$t_1=9.6min$,$t_2=14.4min$。总时长:$45min+9.6min+14.4min+24min=93min$
(1)大
(2)先增大后不变;100
(3)50.4
(4)93
查看更多完整答案,请扫码查看


