《2025年新课程学习与评价四年级数学上册人教版》

三、找出下面各题错误的原因,把序号填在括号里,并改正。
```

248
× 32
────
486
624
────
6626
```
(①)
改正：
```
248
× 32
────
496
744
────
7936
```
```
121
× 14
────
484
121
────
605
```

(②)
改正：
```
121
× 14
────
484
1210
────
1694
```

答案： 三、
(①)
改正：
```
248
× 32
────
496
744
────
7936
```
(②)
改正：
```
121
× 14
────
484
1210
────
1694
```

四、解决问题。
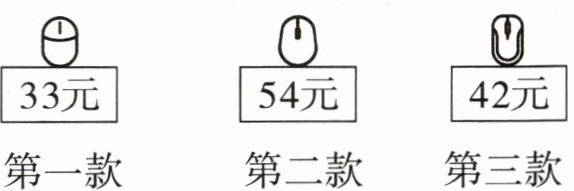
1. 张老师要为学校微机室买 $142$ 个相同的鼠标,他带了 $5000$ 元钱,可以买哪一款？还剩下多少钱？(先估一估,再计算)

2. 刘阿姨所在单位为职工缴存了住房公积金：职工个人每月扣除多少金额,工作单位还要为其缴纳相等的金额。$2022$ 年刘阿姨每月扣除住房公积金 $472$ 元,这一年她的住房公积金账户里将会增加多少钱？(不计利息)

答案： 1.
估算：$142\approx140$，$140×33 = 4620$（元），$140×54=7560$（元）$＞5000$（元），$140×42 = 5880$（元）$＞5000$（元），所以可能买第一款。
计算：$142×33 = 142×(30 + 3)=142×30+142×3=4260+426 = 4686$（元）
$5000 - 4686 = 314$（元）
$142×54 = 142×(50+4)=142×50 + 142×4=7100+568 = 7668$（元）$＞5000$（元）
$142×42 = 142×(40+2)=142×40+142×2=5680 + 284=5964$（元）$＞5000$（元）
可以买第一款，剩下$314$元。
2.
$(472 + 472)×12=944×12 = 11328$（元）
这一年她的住房公积金账户里将会增加$11328$元。

五、在 $□$ 里填上合适的数字,使竖式成立。
```
□ 3 □
× □ 6
──────
2 □ □ 0
□ 7 0
──────
1 □ □ □ 0
```
```
435
× 26
──────
2610
87 0
──────
11310
```

答案： 4,5,2,6,1,8,1,3,1

$2023$ 个 $8$ 连乘的积的个位上的数字与 $2023$ 个 $7$ 连乘的积的个位上的数字相差多少？

答案： 1. 先确定$8$连乘的积的个位数的规律：
$8^1$个位是$8$；$8×8 = 64$，个位是$4$；$4×8 = 32$，个位是$2$；$2×8 = 16$，个位是$6$；$6×8 = 48$，个位是$8$。
周期为$4$，$2023÷4 = 505\cdots\cdots3$，所以$2023$个$8$连乘积的个位数字是$2$。
2. 再确定$7$连乘的积的个位数的规律：
$7^1$个位是$7$；$7×7 = 49$，个位是$9$；$9×7 = 63$，个位是$3$；$3×7 = 21$，个位是$1$；$1×7 = 7$。
周期为$4$，$2023÷4 = 505\cdots\cdots3$，所以$2023$个$7$连乘积的个位数字是$3$。
3. 计算两者差值：
$ |2 - 3|=1$
答：相差$1$。