二、判断。(对的画“√”,错的画“×”)
1. $891234900\approx89123$万 (
2. $891234900\approx9$亿 (
3. $89123490\approx9$万 (
4. $89123490\approx8912$万 (
1. $891234900\approx89123$万 (
√
)2. $891234900\approx9$亿 (
√
)3. $89123490\approx9$万 (
×
)4. $89123490\approx8912$万 (
√
)
答案:
√√×√
三、按要求填一填。
1. $8□6920000\approx8$亿,$□$里可以填(
2. $37□4387600\approx38$亿,$□$里最小填(
3. $4□1658001\approx5$亿,$□$里最大填(
1. $8□6920000\approx8$亿,$□$里可以填(
0,1,2,3,4
)。2. $37□4387600\approx38$亿,$□$里最小填(
5
)。3. $4□1658001\approx5$亿,$□$里最大填(
9
)。
答案:
1. $0$,$1$,$2$,$3$,$4$
2. $5$
3. $9$
2. $5$
3. $9$
四、用 1,2,5,6 和五个 0 组成一个九位数,要使这个数最接近 2 亿,这个数是多少?
答案:
要使组成的九位数最接近2亿,亿位上的数字应为1或2。
情况一:亿位为2
此时需用剩余数字(1,5,6和五个0)组成最小的八位数放在亿位后,使整个数最小(最接近2亿)。剩余数字组成最小八位数时,0尽量靠前,非0数字按从小到大排列,得到200000156。与2亿的差为:200000156 - 200000000 = 156。
情况二:亿位为1
此时需用剩余数字(2,5,6和五个0)组成最大的八位数放在亿位后,使整个数最大(最接近2亿)。剩余数字组成最大八位数时,大数字尽量靠前,得到165200000。与2亿的差为:200000000 - 165200000 = 34800000。
因156 < 34800000,故最接近2亿的数是200000156。
200000156
情况一:亿位为2
此时需用剩余数字(1,5,6和五个0)组成最小的八位数放在亿位后,使整个数最小(最接近2亿)。剩余数字组成最小八位数时,0尽量靠前,非0数字按从小到大排列,得到200000156。与2亿的差为:200000156 - 200000000 = 156。
情况二:亿位为1
此时需用剩余数字(2,5,6和五个0)组成最大的八位数放在亿位后,使整个数最大(最接近2亿)。剩余数字组成最大八位数时,大数字尽量靠前,得到165200000。与2亿的差为:200000000 - 165200000 = 34800000。
因156 < 34800000,故最接近2亿的数是200000156。
200000156
一个九位数,各个数位上的数字之和是 20,这个数最大是多少?最小是多少?
答案:
最大数:
要使九位数最大,需高位数字尽可能大。
亿位最大取9,剩余数字和为20-9=11;
千万位最大取9,剩余数字和为11-9=2;
百万位取2,其余数位为0。
最大数:992000000。
最小数:
要使九位数最小,亿位取1(不能为0),剩余数字和为20-1=19;
低位数字尽可能大,个位、十位各取9(和18),剩余1放百位,其余高位(千万位至千位)为0。
最小数:100000199。
结论:最大是992000000,最小是100000199。
要使九位数最大,需高位数字尽可能大。
亿位最大取9,剩余数字和为20-9=11;
千万位最大取9,剩余数字和为11-9=2;
百万位取2,其余数位为0。
最大数:992000000。
最小数:
要使九位数最小,亿位取1(不能为0),剩余数字和为20-1=19;
低位数字尽可能大,个位、十位各取9(和18),剩余1放百位,其余高位(千万位至千位)为0。
最小数:100000199。
结论:最大是992000000,最小是100000199。
1. 算盘上的1颗上珠表示(
5
),1颗下珠表示(1
)。
答案:
5,1
2. 在电子计算器上,+,-,×,÷统称(
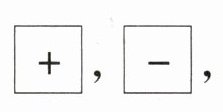

运算符号
)键;ON是(开机
)键;AC是(清除
)键。

答案:
运算符号;开机;清除
3. 用计算器计算87×5时先输入(
87
),再输入(×
),然后输入(5
),最后输入(=
),屏幕出现的数就是计算的结果。
答案:
87,×,5,=
查看更多完整答案,请扫码查看


