《2025年绩优学案七年级数学上册人教版》

1. 数$-3$,0,1,2中,负有理数是(A)
A.$-3$
B.0
C.1
D.2

答案： A

2. 在下列各数：$-3$,2.5,0,$-\frac{2}{5}$,$-0.6$,10中,负分数有(B)
A.1个
B.2个
C.3个
D.4个

答案： B

3. 将$\frac{4}{5}$化成小数是0.8；将0.28化成分数是$\frac{7}{25}$。

答案： $0.8$；$\frac{7}{25}$

4. 写出一个是整数但不是正有理数的数：-1。

答案： -1（答案不唯一，0或其他负整数均可）

5. 在1,$-3.5$,0,$+28\%$,$0.333…$,$-100$这些数中,
整数有：1, 0, -100；
分数有：$-3.5, +28\%, 0.333\ldots$；
正有理数有：$1, +28\%, 0.333\ldots$；
负有理数有：-3.5, -100。

答案： 整数有：1, 0, -100；分数有：$-3.5, +28\%, 0.333\ldots；$正有理数有：$1, +28\%, 0.333\ldots；$负有理数有：-3.5, -100。

6. 下列说法正确的有(B)
(1)整数就是正整数和负整数；(2)零是整数,但不是自然数；(3)分数包括正分数、负分数；(4)正有理数和负有理数统称为有理数；(5)一个有理数,它不是整数就是分数。
A.1个
B.2个
C.3个
D.4个

答案： B

7. 负整数集合是(B)

A.有理数集合中去掉分数和零
B.整数集合中去掉正整数和零
C.整数集合中去掉正整数
D.有理数集合中去掉正有理数和零

答案： B

8. $\{0,1,23,\frac{1}{5},…\}$可以表示的集合是有理数集合。

答案： 有理数集合

9. 把下列各数填入相应的集合中：
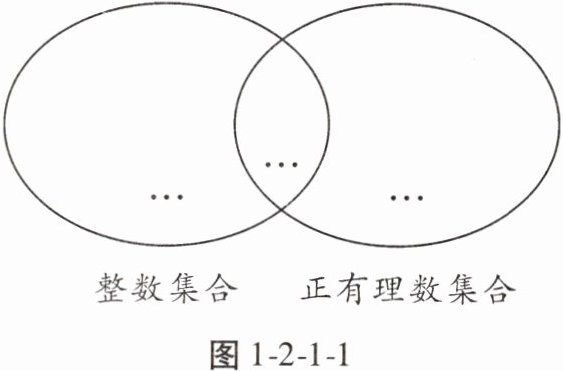
10,$-0.72$,$-2$,0,$-98$,25,20%,3.14,$\frac{1}{2}$。

答案： 整数集合（左图）：$10$，$-2$，$25$（中间与右图重复部分也属于左图），$0$，$-98$；
正有理数集合（右图）：$10$，$25$，$20\%$，$3.14$，$\frac{1}{2}$。

10. 有10个有理数,小明说“其中有6个正有理数”,小红说“其中有6个整数”,小华说“其中正分数的个数与负分数的个数相等”,小林说“负有理数的个数不超过3个”。请你根据4名同学的叙述判断这10个有理数中共有几个负整数。

答案： 1. 正有理数有6个，小华说正分数与负分数个数相等，设正分数、负分数各为a个，分数总数为2a。有理数共10个，整数有6个，故分数有10-6=4个，即2a=4，得a=2，正分数=2，负分数=2。
2. 正有理数=正整数+正分数=6，正分数=2，故正整数=6-2=4。
3. 整数共6个，包括正整数、0、负整数。设负整数为x，正整数=4，整数总数=4+0的个数+x=6，即0的个数+x=2。0的个数为0或1（0是唯一整数）。
4. 负有理数=负整数+负分数=x+2，小林说负有理数≤3，即x+2≤3，得x≤1，x≥0（负整数非负），故x=0或1。
5. 若x=0，则0的个数=2，矛盾（0仅1个）；若x=1，则0的个数=1，符合。
结论：负整数有1个。
1