《2025年绩优学案七年级数学上册人教版》

9. 古希腊毕达哥拉斯学派的“三角形数”是一列点(或圆球)在等距的排列下可以形成正三角形的数,如$1,3,6,10,15,……$我国宋元时期数学家朱世杰在《四元玉鉴》中所记载的“垛积术”其中的“落一形”堆垛就是每层为“三角形数”的三角锥的锥垛(如图,顶上一层$1$个球,下一层$3$个球,再下一层$6个球……$),若一个“落一形”三角锥垛有$10$层,则该堆垛第$n$层球的个数为(D)
[]
A.$n$
B.$2n$
C.$2n + 1$
D.$\frac{1}{2}n(n + 1)$

答案： D

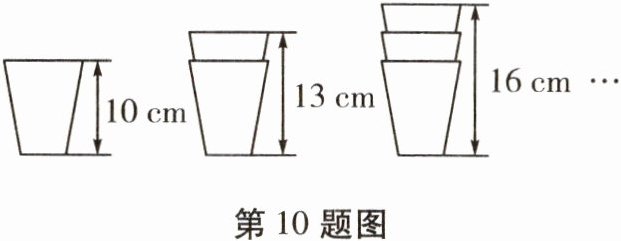
10. 有一种塑料杯子的高度是$10\ cm$,两个以及三个这种杯子叠放时高度如图所示,第$n$个这种杯子叠放在一起的高度是$3n + 7$$cm$(用含$n$的式子表示)。

答案： $3n + 7$

11. 我国古代数学家杨辉在《详解九章算法》一书中辑录了如图所示的三角形,后人称它为“杨辉三角”。它具有一定的规律性,从图中取一斜列数：$1,3,6,10,15$,我们把第一个数记为$a_{1}$,第二个数记为$a_{2}$,第三个数记为$a_{3},……第n个数记为a_{n}$,则$a_{n}$为$\frac{n(n + 1)}{2}$。

答案： $\frac{n(n + 1)}{2}$（由于题目不是选择题，这里按照要求应填写表达式相关的结果，若按照给定格式要求可理解为填写该表达式化简后的代表形式等相关，严格按给定格式这里填$\frac{n(n + 1)}{2}$对应的无选项形式，若从答案呈现角度可认为就是该表达式结果） 。

12. 如图是用棋子摆成的“小屋子”。摆第$1$个这样的“小屋子”需要$5$枚棋子,摆第$2$个这样的“小屋子”需要$11枚棋子……$
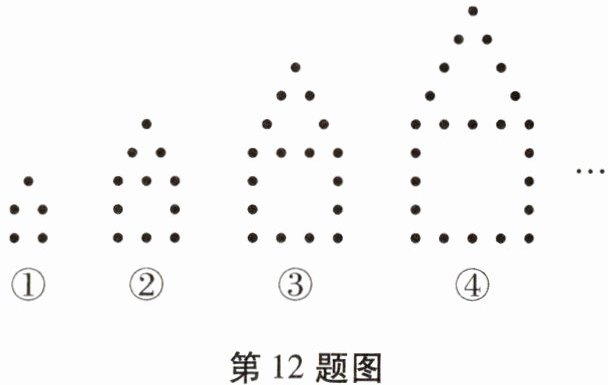
(1)摆第$n$个这样的“小屋子”需要多少枚棋子？
(2)摆第$10$个这样的“小屋子”需要多少枚棋子？

答案：
(1)观察图形可知：
第$1$个图形，共有$5$枚棋子，可写成$6×1 - 1$ $=1 + 4×1$；
第$2$个图形，共有$11$枚棋子，可写成$6×2 - 1=1 + 4 + 6×1 - 4$（从增量角度看，是在第$1$个基础上，屋顶不变，下面增加$6$个棋子再减去重复部分思路，也可直接数出）；更准确从规律看$11 = 6×2 - 1$；
第$3$个图形，棋子数为$17$，$17=6×3 - 1$；
第$4$个图形，棋子数为$23$，$23 = 6×4 - 1$。
则摆第$n$个这样的“小屋子”需要的棋子数为$6n - 1$。
(2)当$n = 10$时，$6n - 1=6×10 - 1=59$。
答：
(1)摆第$n$个这样的“小屋子”需要$(6n - 1)$枚棋子；
(2)摆第$10$个这样的“小屋子”需要$59$枚棋子。