《2025年绩优学案七年级数学上册人教版》

1. 下面几组量不成反比例的是(C)
A.路程一定,时间和速度
B.长方形面积一定,长和宽
C.圆周长一定,圆的直径和圆周率
D.比的前项一定,比的后项和比值

答案： C

2. 下面的三个问题中都有两个变量：
① 总价一定,购物的数量与商品的单价；
② 某村的耕地面积一定,该村人均耕地面积 $S$ 与全村总人口 $n$；
③ 汽车的行驶速度一定,行驶路程 $s$ 与行驶时间 $t$。
其中,两个变量之间的关系是反比例关系的是(A)
A.①②
B.①③
C.②③
D.①②③

答案： A

3. 在物理学中,压强 $p$ 和受力面积 $S$ 以及压力 $F$ 之间的关系式是 $p = \frac{F}{S}$,如果人对地面的压力是 $600 N$。那么,此时压强 $p$ 和受力面积 $S$ 成反比例关系。

答案： 反

4. 已知 $y$ 与 $x$ 成反比例,且当 $x = -3$ 时,$y = 4$,则当 $x = 6$ 时,$y$ 的值为-2。

答案： -2

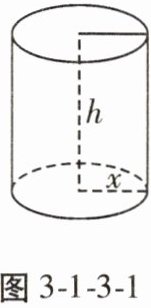
5. 如图 3 - 1 - 3 - 1,圆柱的侧面积为 $10 m^2$。记圆柱的底面半径为 $x m$,高为 $h m$。当 $x$ 在一定范围内变化时,$h$ 随 $x$ 的变化而变化,则 $h$ 与 $x$ 满足的关系式是$h = \frac{5}{\pi x}$。

答案： $h = \frac{5}{\pi x}$

6. 码头工人每天往一艘轮船上装载 $40 t$ 货物,装载完毕恰好用了 $6$ 天时间。轮船到达目的地后开始卸货,平均卸货速度 $v$ 与卸货天数 $t$ 之间的关系式是$v = \frac{240}{t}$。

答案： $v = \frac{240}{t}$。

7. 下面的三个问题中都有两个变量：
① 一个容积固定的游泳池,游泳池注满水的过程中注水速度与所用时间；
② 一个体积固定的长方体,长方体的高与底面积；
③ 平行四边形面积一定时,底与高。
其中,变量与变量之间的关系是反比例关系的是①②③。(填序号)

答案： ①②③

8. 已知 $y$ 与 $x^2$ 成反比例,且当 $x = -2$ 时,$y = 3$,则当 $y = 6$ 时,$x^2$ 的值为2。

答案： $2$（这里按题目要求只需填数值，由于本题是填空形式，按规则直接填结果数值）

9. 蓄水池的排水管每小时排水 $9 m^3$,$5 h$ 可以将满池水全部排空。
(1) 蓄水池的容积是多少？
(2) 如果增加排水管,使每小时的排水量达到 $Q m^3$,那么将满池水排空所需的时间 $t$ 如何变化？
(3) 写出 $t$ 与 $Q$ 之间的关系式。$t$ 与 $Q$ 之间成什么比例关系？

答案：
(1) 蓄水池每小时排水$9 m^3$，5小时排空，所以容积为：
$9 m^3/h × 5 h = 45 m^3$。
(2) 如果每小时排水量增加到$Q m^3$，排空时间$t$会相应减少，因为总容积不变，排水速度加快，所以所需时间减少。
(3) 根据容积=排水速度$×$时间，得到：
$Q \cdot t = 45$
即：
$t = \frac{45}{Q}$
$t$与$Q$之间的关系是反比例关系。