《2025年绩优学案七年级数学上册人教版》

2. 下列说法错误的是 (D)

A.开启计算器使之工作的按键是$\boxed{ON}$键

B.输入$-5.8的按键顺序是\boxed{(-)}$$\boxed{5}$$\boxed{·}$$\boxed{8}$
C.输入$0.58的按键顺序是\boxed{·}$$\boxed{5}$$\boxed{8}$
 D.按键$\boxed{6}$$\boxed{9}$$\boxed{(-)}$$\boxed{8}$$\boxed{7}$$\boxed{=}能计算-69 - 87$的结果

答案： D

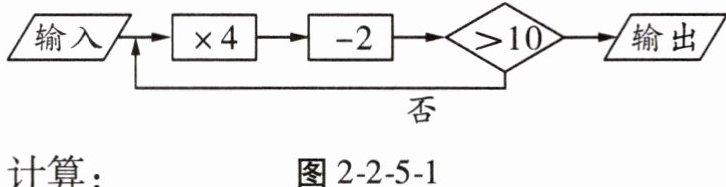
3. 如图2-2-5-1为计算机某计算程序,若开始输入3,则最后输出的结果是38。

答案： 38

4. 计算：
(1) $20 - 8÷(-4)×(-0.25)$；
(2) $-16\frac{2}{3} + (-8)÷4 - (-4)×(+\frac{2}{3})$。

答案：
(1) $20 - 8÷(-4)×(-0.25)$
$=20 - (-2)×(-0.25)$
$=20 - 0.5$
$=19.5$
(2) $-16\frac{2}{3} + (-8)÷4 - (-4)×(+\frac{2}{3})$
$=-\frac{50}{3} + (-2) - (-\frac{8}{3})$
$=-\frac{50}{3} - 2 + \frac{8}{3}$
$=(-\frac{50}{3} + \frac{8}{3}) - 2$
$=-\frac{42}{3} - 2$
$=-14 - 2$
$=-16$

5. 下列计算结果正确的是 (D)
A.$1 + (-24\frac{6}{7})÷(-6) = -3\frac{1}{7}$
B.$-3.5÷\frac{7}{8}×(-\frac{3}{4}) - 2 = -5$
C.$(-\frac{3}{5})÷(-\frac{9}{16})×16 = \frac{1}{3}$
D.$3 - (-6)÷(-4)÷1\frac{1}{5} = \frac{7}{4}$

答案： D

6. 若$x$,$y$互为相反数,$a$,$b$互为倒数,且$m$的绝对值是2,则$3x + 3y - 2ab + m$的值是0或-4。

答案： $0$或$-4$（或写成对应的填空形式，由于本题为填空题，直接给出数值即可）

7. 根据试验测定：高度每增加1 km,气温大约降低6℃。某登山运动员在攀登某山峰的途中发回信息,报告他所在高度的气温为$-15℃$。如果当时地面温度为$3℃$,那么该登山运动员所在位置的高度是多少？

答案： 解：根据题意，地面温度与运动员所在高度的气温之差为：
$3 - (-15) = 18（℃）$。
由于高度每增加1 km，气温降低6℃，所以运动员所在位置的高度为：
$\frac{18}{6} = 3（km）$。
答：该登山运动员所在位置的高度是3 km。

8. 阅读材料：计算$\frac{1}{30}÷(\frac{2}{3} - \frac{1}{10} + \frac{1}{6} - \frac{2}{5})$。
解：原式的倒数是$(\frac{2}{3} - \frac{1}{10} + \frac{1}{6} - \frac{2}{5})×30$
$=\frac{2}{3}×30 - \frac{1}{10}×30 + \frac{1}{6}×30 - \frac{2}{5}×30 = 10$,
故原式$=\frac{1}{10}$。
请你根据以上材料,选择合适的方法计算：$\frac{1}{48}÷(\frac{1}{12} - \frac{3}{16} + \frac{5}{24} + \frac{2}{3})$。

答案： 解：原式的倒数是$(\frac{1}{12} - \frac{3}{16} + \frac{5}{24} + \frac{2}{3})×48$
$=\frac{1}{12}×48 - \frac{3}{16}×48 + \frac{5}{24}×48 + \frac{2}{3}×48$
$=4 - 9 + 10 + 32$
$=37$
故原式$=\frac{1}{37}$