《2025年新课程学习与测评同步学习八年级数学上册人教版》

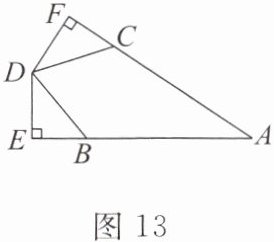
6. 如图13,AB= AC,BD= CD,DE⊥AB于点E,DF⊥AC于点F,求证DE= DF.

答案：
证明:如图28,连接AD.在△ABD和△ACD中,$\left\{\begin{array}{l}AB=AC,\\ BD=CD,\\ AD=AD,\end{array}\right.$
∴　　△ABD≌△ACD(SSS).
∴　　∠BAD=∠CAD,即AD平分∠EAF.又
∵　　DE⊥AB,DF⊥AC,
∴　DE=DF.

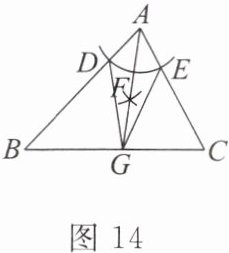
7. [2023浙江衢州中考]如图14,在△ABC中,以点A为圆心,适当长为半径作弧,分别交AB,AC于点D,E.分别以点D,E为圆心,大于$\frac{1}{2}DE$长为半径作弧,交于∠BAC内一点F.连接AF并延长,交BC于点G.连接DG,EG.添加下列条件,不能使BG= CG成立的是(D).

A.AB= AC
B.AG⊥BC
C.∠DGB= ∠EGC
D.AG= AC

答案： D　　提示:根据题中所给的作图步骤可知,AG是△ABC的角平分线,即∠BAG=∠CAG.当AB=AC时,又∠BAG=∠CAG,AG=AG,所以△ABG≌△ACG(SAS).所以BG=CG.故选项A不符合题意.当AG⊥BC时,∠AGB=∠AGC=90°,又∠BAG=∠CAG,AG=AG,所以△ABG≌△ACG(ASA).所以BG=CG.故选项B不符合题意.因为AD=AE,∠BAG=∠CAG,AG=AG,所以△ADG≌△AEG(SAS).所以∠AGD=∠AGE.又∠DGB=∠EGC,所以∠AGD+∠DGB=∠AGE+∠EGC,即∠AGB=∠AGC.又∠AGB+∠AGC=180°,所以∠AGB=∠AGC=90°.则同理可得出BG=CG,故选项C不符合题意.

8. 项目式学习
【项目主题】确定三角形菜园的小门位置.
【项目背景】某中学积极响应劳动教育的号召,在校园内开辟了一处“青禾”劳动实践基地.八年级1班负责管理一块形状为三角形的菜园.为了便于同学们日常进出浇水、施肥、采摘,同时最大程度避免踩踏菜地,班级劳动委员会决定在菜园靠路的一边修建一扇小门.现需要设计的施工图纸.
【方案设计】第一步：绘制三角形菜园示意图△ABC；
第二步：确定菜园小门的位置.
为确保通行便利和安全,希望小门的位置(点D)在靠路的一边AB上,且到菜园另外两边(AC和BC)的距离相等.
【方案实施】(1)根据测量获得菜园的两个内角∠α,∠β及其夹边长度(按比例缩至图纸尺寸为线段a),如图15所示.请你利用直尺和圆规作出△ABC(其中∠A= ∠α,∠B= ∠β,AB= a).
(2)根据【方案设计】中的第二步,在(1)中所作的△ABC中用直尺和圆规确定小门的位置(点D).
(要求：保留作图痕迹,标注字母,不写作法)

答案：
解:
(1)如图29,△ABC就是所求作的三角形
(2)如图29,点D就是所求小门的位置.